��Ŀ����
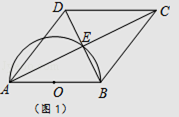
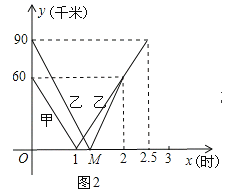
����Ŀ����ͼ,��һ����ֱ�ع�·����A,B,C����,,�������150km,�ס������������ֱ��B,C����ͬʱ����,�ع�·�����������,�ֱ�ʻ��C,B����.�ס���������A�صľ���y1��y2����ʻʱ��x(h)�ĺ���ͼ����ͼ2��ʾ.(��:����)
(1)����ͼ1�б��A�صĴ���λ��;
(2)ͼ2��,M���������_________,�õ��ʵ��������_________;
(3)��׳���A�صľ���![]() ����ʻʱ��
����ʻʱ��![]() �ĺ�����ϵʽ,ֱ��д���ҳ���A�صľ���y2����ʻʱ��
�ĺ�����ϵʽ,ֱ��д���ҳ���A�صľ���y2����ʻʱ��![]() �ĺ�����ϵʽ,����ͼ2�в�ȫ�׳��ĺ���ͼ��;
�ĺ�����ϵʽ,����ͼ2�в�ȫ�׳��ĺ���ͼ��;
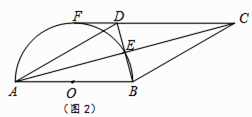
(4)A������ָ������,ָ���������������жԽ���,�����Խ�����֮15km��(��15km)ʱ�ܹ�����ͨ��,ֱ��д����������ͬʱ��ָ�������öԽ���ͨ����ʱ��.


���𰸡���1�������������2����1.2��0������M��ʾ�ҳ�1.2Сʱ����A�أ���3���ף�0��x��1ʱ��y1=-60x+60��1��x��2.5ʱ��y1=60x-60���ң�0��x��1.2ʱ��y2=-75x+90��1.2��x��2ʱ��y2=75x-90��ͼ�����������4��![]() Сʱ.
Сʱ.
����������������� ��1������ͼ��ɵ�AB=60ǧ�ף�CA=90ǧ�ף�����AB��AC=2��3ȷ������A��λ�ü��ɣ���2��ֱ�Ӹ���������ʽ�����ҳ����ٶ�150��2=75ǧ��/ʱ��90��75=1.2�����Ե�M��ʾ�ҳ�1.2Сʱ����A�أ��ɴ˼�����⣻��3������ͼ���֪ͼ���ϵ�����꣬���������Ա���ȡֵ��Χ���������ϵʽ���ɣ���4�����ݡ������Խ�����15ǧ��֮�ڣ���15ǧ�ף�ʱ�ܹ�����ͨ������Ϊ���ȹ�ϵ�в���ʽ�飬��⼴�ɵõ�ͨ����ʱ�䷶Χ������������ͬʱ��ָ������ͨ����ʱ�䣮
���������
��1��A��λ����ͼ��ʾ��ʹ��A����AB��AC=2��3��
![]()
��2���ҳ����ٶ�150��2=75ǧ��/ʱ��
90��75=1.2��
��M��1.2��0����
���Ե�M��ʾ�ҳ�1.2Сʱ����A�أ�
��3���׳��ĺ���ͼ����ͼ��ʾ���׳����ٶ�60��1=60��ǧ��/ʱ����
�׳���B��C����ʱ��Ϊ��150��60=2.5��Сʱ����
����0��60������1��0��������y1=kx+b��
�ã� ![]() ��
��
��ã� ![]() ��
��
�ʵ�0��x��1ʱ��y1=-60x+60��
����2.5��90������1��0��������y1=ax+c��
![]() ��
��
��ã�
![]() .
.
�ʵ�1��x��2.5ʱ��y1=60x-60��
�ҳ���A�صľ���y2����ʻʱ��x��h���ĺ�����ϵʽΪ��
����0��90������1.2��0��������y2=dx+e��
![]() ��
��
��ã� ![]() ��
��
�ʵ�0��x��1.2ʱ��y2=-75x+90��
����2��60������1.2��0��������y2=fx+r��
![]() ��
��
��ã� ![]() ��
��
�ʵ�1.2��x��2ʱ��y2=75x-90��
��ͼ��ʾ��
 ��
��
��4��������ü׳���ָ�����ĵ�ͨ��ʱ��Ϊ�� ![]() ��
��
��![]() ��x��
��x��![]() ��
��
�ҳ���ָ�����ĵ�ͨ��ʱ�䣺
![]() ��
��
��1��x��![]() ��
��
��1��x��![]() ��
��
������ͬʱ��ָ������ͨ����ʱ��Ϊ: ![]() -1=
-1=![]() Сʱ��
Сʱ��

 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�����Ŀ��ij��˾��![]() ���ֿ�ֱ��л���16̨��12̨����Ҫ�����ס������أ����м���Ҫ15̨���ҵ���Ҫ13̨����֪
���ֿ�ֱ��л���16̨��12̨����Ҫ�����ס������أ����м���Ҫ15̨���ҵ���Ҫ13̨����֪![]() ���زֿ������ף������ػ����ķ���������������ʾ��
���زֿ������ף������ػ����ķ���������������ʾ��
![]() ���A�ֿ��x̨����ȥ�أ����ú�x�Ĵ���ʽ��ȫ������ұ���
���A�ֿ��x̨����ȥ�أ����ú�x�Ĵ���ʽ��ȫ������ұ���
�������˷��ñ��������˷�����
������ Ŀ�ĵ��˷� | A | B | ������ Ŀ�ĵ����� | A | B | �ϼ� | |
�� | 500 | 300 | �� | x | 15 | ||
�� | 400 | 600 | �ҵ� | 13 | |||
�ϼ� | 16 | 12 | 28 |
![]() �����˷�ΪyԪ����y��x֮��ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
�����˷�ΪyԪ����y��x֮��ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
![]() �ɻ������˷�������֪����n�ֵ��˷�������n��ֵ��
�ɻ������˷�������֪����n�ֵ��˷�������n��ֵ��