题目内容
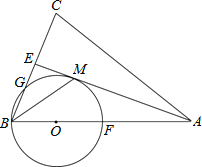
【题目】如图,AB是⊙O直径,直径AB⊥弦CD于点E,四边形ADCF是平行四边形,CD=4![]() ,BE=2.
,BE=2.

(1)求⊙O直径和弦AD的长;
(2)求证:FC是⊙O切线.
【答案】(1)⊙O直径为8,弦AD长为4![]() .(2)见解析
.(2)见解析
【解析】
试题分析:(1)设⊙O的半径为r,连接OC,则OC=r,OE=r﹣2,根据垂径定理得到CE=![]() CD=2
CD=2![]() ,然后根据勾股定理得到r2=(r﹣2)2+(2
,然后根据勾股定理得到r2=(r﹣2)2+(2![]() )2,求得r=4,从而求得AE=6,在Rt△AED中,根据勾股定理即可求得AD;
)2,求得r=4,从而求得AE=6,在Rt△AED中,根据勾股定理即可求得AD;
(2)连结OF,由四边形ABCD是平行四边形得到AF∥DC,则AB⊥AF,即:∠FAO=90°,然后证得平行四边形ADCF是菱形,得出FC=AF,证得△FCO≌△FAO,得出根据切线的判定得到∠FCO=∠FAO=90°,即可证得FC为⊙O的切线.
解:(1)设⊙O的半径为r,连接OC,则OC=r,OE=r﹣2
∵直径AB⊥弦CD
∴CE=![]() CD=
CD=![]() ×4
×4![]() =2
=2![]() ,
,
在Rt△OCE中:OC2=CE2+OE2 即:r2=(r﹣2)2+(2![]() )2,
)2,
解得:r=4,
∴AE=2×4﹣2=6,
在Rt△AED中:AD=![]() =
=![]() =4
=4![]() ,
,
∴⊙O直径为8,弦AD长为4![]() .
.
(2)连结OF,
∵平行四边形ADCF中AF∥CD
又∵AB⊥CD,
∴AB⊥AF,即:∠FAO=90°,
由(1)可知AD=CD=4![]() ,
,
∴平行四边形ADCF是菱形,
∴FC=AF,
在△FCO和△FAO中,
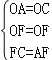
∴△FCO≌△FAO(SSS),
∴∠FCO=∠FAO=90°即:OC⊥FC
∴FC是⊙O切线.


练习册系列答案
相关题目