题目内容
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
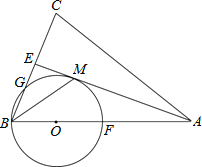
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.
【答案】(1)见解析;(2)3;(3)2
【解析】
试题分析:(1)连接OM.利用角平分线的性质和平行线的性质得到AE⊥OM后即可证得AE是⊙O的切线;
(2)设⊙O的半径为R,根据OM∥BE,得到△OMA∽△BEA,利用平行线的性质得到![]() =
=![]() ,即可解得R=3,从而求得⊙O的半径为3;
,即可解得R=3,从而求得⊙O的半径为3;
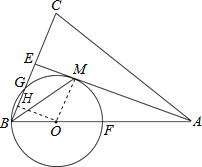
(3)过点O作OH⊥BG于点H,则BG=2BH,根据∠OME=∠MEH=∠EHO=90°,得到四边形OMEH是矩形,从而得到HE=OM=3和BH=1,证得结论BG=2BH=2.
(1)证明:连接OM.
∵AC=AB,AE平分∠BAC,
∴AE⊥BC,CE=BE=![]() BC=4,
BC=4,
∵OB=OM,
∴∠OBM=∠OMB,
∵BM平分∠ABC,
∴∠OBM=∠CBM,
∴∠OMB=∠CBM,
∴OM∥BC
又∵AE⊥BC,
∴AE⊥OM,
∴AE是⊙O的切线;
(2)设⊙O的半径为R,
∵OM∥BE,
∴△OMA∽△BEA,
∴![]() =
=![]() 即
即![]() =
=![]() ,
,
解得R=3,
∴⊙O的半径为3;
(3)过点O作OH⊥BG于点H,则BG=2BH,
∵∠OME=∠MEH=∠EHO=90°,
∴四边形OMEH是矩形,
∴HE=OM=3,
∴BH=1,
∴BG=2BH=2.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目