题目内容
如图①,在Rt△AOB中,∠AOB=90°,AB=5,cosA=
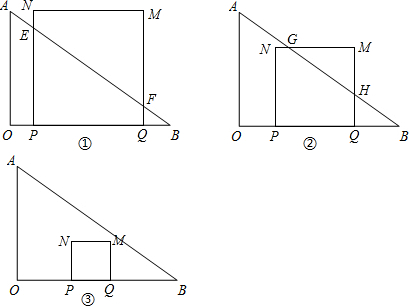
.一动点P从点O出发,以每秒1个单位长度的速度沿OB方向匀速运动;另一动点Q从点B出发,以每秒1个单位长度的速度沿BO方向匀速运动.两动点同时出发,当第一次相遇时即停止运动.在点P、Q运动的过程中,以PQ为一边作正方形PQMN,使正方形PQMN和△AOB在线段OB的同侧.设运动时间为t(单位:秒).

(1)求OA和OB的长度;
(2)在点P、Q运动的过程中,设正方形PQMN和△AOB重叠部分的面积为S,请直接写出S与t之间的函数关系式以及相应的自变量t的取值范围;
(3)如图②,现以△AOB的直角边OB为x轴,顶点O为原点建立平面直角坐标系xOy.取OB的中点C,将过点A、C、B的抛物线记为抛物线T.
①求抛物线T的函数解析式;
②设抛物线T的顶点为点D.在点P、Q运动的过程中,设正方形PQMN的对角线PM、QN交于点E,连接DE、DN.是否存在这样的t,使得△DEN是以EN、DE为两腰或以EN、DN为两腰的等腰三角形?若存在,请求出对应的t的值;若不存在,请说明理由.
| 3 | 5 |

(1)求OA和OB的长度;
(2)在点P、Q运动的过程中,设正方形PQMN和△AOB重叠部分的面积为S,请直接写出S与t之间的函数关系式以及相应的自变量t的取值范围;
(3)如图②,现以△AOB的直角边OB为x轴,顶点O为原点建立平面直角坐标系xOy.取OB的中点C,将过点A、C、B的抛物线记为抛物线T.
①求抛物线T的函数解析式;
②设抛物线T的顶点为点D.在点P、Q运动的过程中,设正方形PQMN的对角线PM、QN交于点E,连接DE、DN.是否存在这样的t,使得△DEN是以EN、DE为两腰或以EN、DN为两腰的等腰三角形?若存在,请求出对应的t的值;若不存在,请说明理由.
分析:(1)在Rt△AOB中,已知斜边长和∠ABO的余弦值,通过解直角三角形可得出OA、OB的长.
(2)由于正方形、△AOB的重叠部分的形状会随t的变化而变化,因此要先找出关键点:①点N在AB上,②点M在AB上;然后分三种情况讨论:
①边PN与AB有交点时,此时正方形、△AOB的重叠部分是梯形,首先找出梯形两底所在直角三角形,通过解直角三角形求出它们的长,然后通过梯形面积公式解答;
②边PN与AB无交点,但PN与AB有交点时,此时重叠部分是五边形,在求这一部分的面积时,可令正方形的面积减去右上角的小直角三角形的面积;
③当正方形完全在△AOB内部时,重叠部分的面积即正方形的面积.
(3)①在(1)中求得了OB的长,则OC长可得,在确定A、B、C三点坐标的情况下,利用待定系数法即可确定该抛物线的解析式.
②该题的计算过程较为复杂,但思路比较简单,首先求出点D的坐标,然后通过构建直角三角形,利用勾股定理求出△DEN的三边长,然后分①EN=DE、②EN=DN两种情况求出t的值.
(2)由于正方形、△AOB的重叠部分的形状会随t的变化而变化,因此要先找出关键点:①点N在AB上,②点M在AB上;然后分三种情况讨论:
①边PN与AB有交点时,此时正方形、△AOB的重叠部分是梯形,首先找出梯形两底所在直角三角形,通过解直角三角形求出它们的长,然后通过梯形面积公式解答;
②边PN与AB无交点,但PN与AB有交点时,此时重叠部分是五边形,在求这一部分的面积时,可令正方形的面积减去右上角的小直角三角形的面积;
③当正方形完全在△AOB内部时,重叠部分的面积即正方形的面积.
(3)①在(1)中求得了OB的长,则OC长可得,在确定A、B、C三点坐标的情况下,利用待定系数法即可确定该抛物线的解析式.
②该题的计算过程较为复杂,但思路比较简单,首先求出点D的坐标,然后通过构建直角三角形,利用勾股定理求出△DEN的三边长,然后分①EN=DE、②EN=DN两种情况求出t的值.
解答:解:(1)∵cosA=
,AB=5,
∴在Rt△AOB中,cosA=
=
=
,
∴OA=3.
∴在Rt△AOB中,OB=
=4.
∴OA的长度为3,OB的长度为4.
 (2)Rt△AOB中,AO=3,OB=4,tan∠ABO=
(2)Rt△AOB中,AO=3,OB=4,tan∠ABO=
,cot∠ABO=
;
①当0≤t<
时,如右图①,OP=QB=t,PQ=4-2t;
Rt△EQB中,EQ=QB•tan∠ABO=
t,同理可得:EP=3-
t;
∴S=
(EP+FQ)•PQ=
×3×(4-2t)=6-3t;
②当
≤t<
时,如右图②;
QH=QB•tan∠ABO=
t,MQ=PQ=4-2t,MH=MQ-HQ=4-
t,MG=MH•cot∠MGH=MH•cot∠ABO=
-
t;
S=S正方形PQMN-S△GMH=(4-2t)2-
(4-
t)(
-
t)=-
t2-
t+
;
③当
≤t<2时,如右图③;
S=S正方形PQMN=(4-2t)2=4t2-16t+16;
综上,可得:
当0≤t<
时,S=6-3t.
当
≤t<
时,S=-
t2-
t+
.
当
≤t<2时,S=4t2-16t+16.
(3)①∵点C为OB的中点,∴OC=BC=
OB=
×4=2.
∴点C的坐标为(2,0).
∵抛物线T经过A(0,3)、B(2,0)、C(4,0)三点,
∴
,
解得:
∴抛物线T的解析式为y=
x2-
x+3.
②存在.理由如下:
∵抛物线T的解析式为y=
x2-
x+3,即y=
(x-3)2-
.
∴抛物线T的顶点D的坐标为(3,-
).
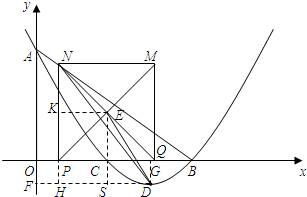 过点D作DF⊥y轴于点F,过点D作DG⊥x轴于点G,延长NP交DF于点H,过点E作EK⊥PN于点K,过点E作ES⊥DF于点S.
过点D作DF⊥y轴于点F,过点D作DG⊥x轴于点G,延长NP交DF于点H,过点E作EK⊥PN于点K,过点E作ES⊥DF于点S.
∵点D的坐标为(3,-
),
∴DF=OG=3,DG=-(-
)=
.
易知CS=PH=DG=
∵由题意知OP=BQ=t,
∴PQ=OB-OP-BQ=4-2t.
∵正方形PQMN已知,
∴PN=PQ=4-2t,∠PNQ=45°,EP=EN=EQ=
NQ.
∴在Rt△NPQ中,cos∠PNQ=cos45°=
=
=
,
∴NQ=4
-2
t.
∴EN=EQ=
NQ=
(4
-2
t)=2
-
t.
∴EN2=(2
-
t)2=2t2-8t+8.
易知FH=OP=t,
∴DH=DF-FH=3-t,NH=NP+PH=4-2t+
=
-2t.
∴在Rt△DHN中,DN2=DH2+NH2=(3-t)2+(
-2t)2=5t2-
t+
.
∵EN=EP,EK⊥NP,
∴NK=PK=
NP=
(4-2t)=2-t.
∵点E是正方形PQMN的对角线的交点,
∴ES是PQ的垂直平分线.
∴ES是OB的垂直平分线.
∵点C是OB的中点,
∴E、C、S三点共线.
∴易知CE=PK=2-t.
∴ES=CE+CS=2-t+
=
-t.
∵CG=OG-OC=3-2=1.
易知DS=CG=1.
∴在Rt△DES中,DE2=ES2+DS2=(
-t)2+12=t2-
t+
.
(ⅰ)当EN=DE时,EN2=DE2,
即2t2-8t+8=t2-
t+
.
解得t1=
,t2=
.
由(2)知,0≤t<2,而
>2,故t2=
舍去.
(ⅱ)当EN=DN时,NE2=DN2,
即2t2-8t+8=5t2-
t+
.整理,得3t2-
t+
=0.
△=b2-4ac=(-
)2-4×3×
=-
<0,
故此一元二次方程无解.
故使得EN=DN的t值不存在.
综上所述,共存在1个这样的t值,使得△DEN是以EN、DE为两腰的等腰三角形,即t=
.
| 3 |
| 5 |
∴在Rt△AOB中,cosA=
| OA |
| AB |
| OA |
| 5 |
| 3 |
| 5 |
∴OA=3.
∴在Rt△AOB中,OB=
| AB2-OA2 |
∴OA的长度为3,OB的长度为4.
 (2)Rt△AOB中,AO=3,OB=4,tan∠ABO=
(2)Rt△AOB中,AO=3,OB=4,tan∠ABO=| 3 |
| 4 |
| 4 |
| 3 |
①当0≤t<
| 4 |
| 5 |
Rt△EQB中,EQ=QB•tan∠ABO=
| 3 |
| 4 |
| 3 |
| 4 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
②当
| 4 |
| 5 |
| 16 |
| 11 |
QH=QB•tan∠ABO=
| 3 |
| 4 |
| 11 |
| 4 |
| 16 |
| 3 |
| 11 |
| 3 |
S=S正方形PQMN-S△GMH=(4-2t)2-
| 1 |
| 2 |
| 11 |
| 4 |
| 16 |
| 3 |
| 11 |
| 3 |
| 25 |
| 24 |
| 4 |
| 3 |
| 16 |
| 3 |
③当
| 16 |
| 11 |
S=S正方形PQMN=(4-2t)2=4t2-16t+16;
综上,可得:
当0≤t<
| 4 |
| 5 |
当
| 4 |
| 5 |
| 16 |
| 11 |
| 25 |
| 24 |
| 4 |
| 3 |
| 16 |
| 3 |
当
| 16 |
| 11 |
(3)①∵点C为OB的中点,∴OC=BC=
| 1 |
| 2 |
| 1 |
| 2 |
∴点C的坐标为(2,0).
∵抛物线T经过A(0,3)、B(2,0)、C(4,0)三点,
∴
|
解得:
|
∴抛物线T的解析式为y=
| 3 |
| 8 |
| 9 |
| 4 |
②存在.理由如下:
∵抛物线T的解析式为y=
| 3 |
| 8 |
| 9 |
| 4 |
| 3 |
| 8 |
| 3 |
| 8 |
∴抛物线T的顶点D的坐标为(3,-
| 3 |
| 8 |
 过点D作DF⊥y轴于点F,过点D作DG⊥x轴于点G,延长NP交DF于点H,过点E作EK⊥PN于点K,过点E作ES⊥DF于点S.
过点D作DF⊥y轴于点F,过点D作DG⊥x轴于点G,延长NP交DF于点H,过点E作EK⊥PN于点K,过点E作ES⊥DF于点S.∵点D的坐标为(3,-
| 3 |
| 8 |
∴DF=OG=3,DG=-(-
| 3 |
| 8 |
| 3 |
| 8 |
易知CS=PH=DG=
| 3 |
| 8 |
∵由题意知OP=BQ=t,
∴PQ=OB-OP-BQ=4-2t.
∵正方形PQMN已知,
∴PN=PQ=4-2t,∠PNQ=45°,EP=EN=EQ=
| 1 |
| 2 |
∴在Rt△NPQ中,cos∠PNQ=cos45°=
| ||
| 2 |
| PN |
| NQ |
| 4-2t |
| NQ |
∴NQ=4
| 2 |
| 2 |
∴EN=EQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∴EN2=(2
| 2 |
| 2 |
易知FH=OP=t,
∴DH=DF-FH=3-t,NH=NP+PH=4-2t+
| 3 |
| 8 |
| 35 |
| 8 |
∴在Rt△DHN中,DN2=DH2+NH2=(3-t)2+(
| 35 |
| 8 |
| 47 |
| 2 |
| 1801 |
| 64 |
∵EN=EP,EK⊥NP,
∴NK=PK=
| 1 |
| 2 |
| 1 |
| 2 |
∵点E是正方形PQMN的对角线的交点,
∴ES是PQ的垂直平分线.
∴ES是OB的垂直平分线.
∵点C是OB的中点,
∴E、C、S三点共线.
∴易知CE=PK=2-t.
∴ES=CE+CS=2-t+
| 3 |
| 8 |
| 19 |
| 8 |
∵CG=OG-OC=3-2=1.
易知DS=CG=1.
∴在Rt△DES中,DE2=ES2+DS2=(
| 19 |
| 8 |
| 19 |
| 4 |
| 425 |
| 64 |
(ⅰ)当EN=DE时,EN2=DE2,
即2t2-8t+8=t2-
| 19 |
| 4 |
| 425 |
| 64 |
解得t1=
13-
| ||
| 8 |
13+
| ||
| 8 |
由(2)知,0≤t<2,而
13+
| ||
| 8 |
13+
| ||
| 8 |
(ⅱ)当EN=DN时,NE2=DN2,
即2t2-8t+8=5t2-
| 47 |
| 2 |
| 1801 |
| 64 |
| 31 |
| 2 |
| 1289 |
| 64 |
△=b2-4ac=(-
| 31 |
| 2 |
| 1289 |
| 64 |
| 23 |
| 16 |
故此一元二次方程无解.
故使得EN=DN的t值不存在.
综上所述,共存在1个这样的t值,使得△DEN是以EN、DE为两腰的等腰三角形,即t=
13-
| ||
| 8 |
点评:该题是难度较大的图形动点问题,综合了二次函数、正方形的性质、解直角三角形、图形的面积问题等知识.(2)题中,一定要先抓住关键“点”,然后再进行分段讨论.

练习册系列答案
相关题目
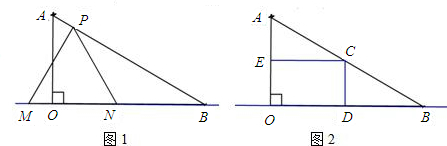

 ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
 ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
 ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.