题目内容
如图1,在Rt△AOB中,∠AOB=90°,AO=4| 3 |
| 3 |
(1)求当等边△PMN的顶点M运动到与点O重合时t的值.
(2)求等边△PMN的边长(用t的代数式表示);
(3)如果取OB的中点D,以OD为边在Rt△AOB 内部作如图2所示的矩形ODCE,点C在线段AB上.设等边△PMN和矩形ODCE重叠部分的面积为S,请求出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
(4)在(3)中,设PN与EC的交点为R,是否存在点R,使△ODR是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由.
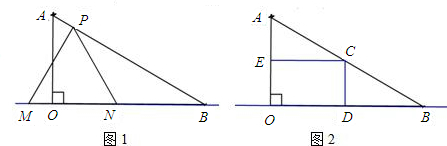
分析:(1)利用直角三角形中30°所对的边是斜边的一半即可求出AP,进而求出t的值;
(2)利用△BPH∽△BAO,得出PH的长,再利用解直角三角形求出PN的长;
(3)根据当0≤t≤1时以及当t=1时和当t=2时,分别求出S的值;
(4)根据当D为顶点,OD=OR1=6时,当R2为顶点,OR2=DR2时,③当O为等腰△的顶点时,分别得出即可.
(2)利用△BPH∽△BAO,得出PH的长,再利用解直角三角形求出PN的长;
(3)根据当0≤t≤1时以及当t=1时和当t=2时,分别求出S的值;
(4)根据当D为顶点,OD=OR1=6时,当R2为顶点,OR2=DR2时,③当O为等腰△的顶点时,分别得出即可.
解答: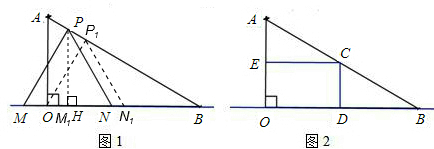 解:(1)∵△PMN是等边三角形,
解:(1)∵△PMN是等边三角形,
∴∠P1M1N1=60°;
∵在Rt△AOB中,
∠AOB=90°,∠ABO=30°,
∴∠AP10=90°,
在Rt△AP1O中,AP1=
AO=2
,
∴t=
,即t=2;
(2)∵△BPH∽△BAO,
∴
=
,
∴PH=
,
∵cos30°=
,
∴PN=
=
=8-t,
(3)当0≤t≤1时,S1=S四边形EONG,
作GH⊥OB于H,如图3,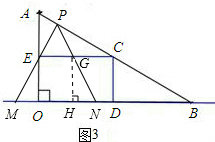
∵∠GNH=60°,GH=2
,
∴HN=2,∵PN=NB=8-t,
∴ON=OB-NB,
∴ON=12-(8-t)=4+t,
∴OH=4+t-2=2+t,
S1=
(2+t+4+t)×2
=2
t+6
,
∵2
>0,
∴S随t增大而增大,
当t=1时,S最大=8
,
当1<t<2时,如图4,S2=S五边形IFONG,
作GH⊥OB于H,
∵AP2=
t
∴AF=2
t,
∴OF=4
-2
t,
∴EF=2
-(4
-2
t)
=2
t-2
,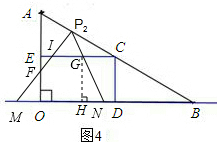
∴EI=2t-2,
∴S2=S梯形EONG-S△EFI
=2
t+6
-
(2t-2)×(2
t-2
)
=-2
t2+6
t+4
,
∵-2
<0,
∴当t=-
=
时
S2最大=
,
当t=2时,如图5,
MP=MN=6,
N与D重合,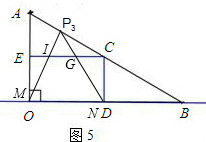
S3=S梯形IMNG,
=
×36-
×4,
=8
,
∴S=
,
S最大=
,
(4)∵△ODR是等腰三角形,
①当D为顶点,OD=OR1=6时,
DR1=6-2
>2(不合题意舍去),
当D为顶点时,R1不存在,
此时R1不存在,使△ODR是等腰三角形,
②当R2为顶点,OR2=DR2时,
R2在EC的中点处,
∵AO=4
,∠B=30°,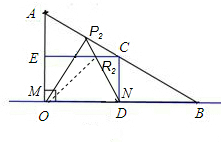
∴BO=12,
∵D为OB中点,
∴DO=EC=6,
∴ER2=3,
∵OB=12,∠B=30°,
∴OP2=6,
∴R2P2=3,
∴ER2=P2R2=3,
∴CP2=3
,
∴AP2=4
-3
=
,
t2=
=1,
③当O为等腰三角形顶角的顶点时,
CR3=6-2
,
CP3=
×
×2=6
-6
,
AP3=4
-(6
-6
),
=6
-2
,
∴t3=
=2
-2>2(不合题意舍去).
综上所述:t=1时,△ODR是等腰三角形.
 解:(1)∵△PMN是等边三角形,
解:(1)∵△PMN是等边三角形,∴∠P1M1N1=60°;
∵在Rt△AOB中,
∠AOB=90°,∠ABO=30°,
∴∠AP10=90°,
在Rt△AP1O中,AP1=
| 1 |
| 2 |
| 3 |
∴t=
2
| ||
|
(2)∵△BPH∽△BAO,
∴
| PH | ||
4
|
8
| ||||
8
|
∴PH=
8
| ||||
| 2 |
∵cos30°=
| PH |
| PN |
∴PN=
| PH |
| cos30° |
| ||||||
|
(3)当0≤t≤1时,S1=S四边形EONG,
作GH⊥OB于H,如图3,

∵∠GNH=60°,GH=2
| 3 |
∴HN=2,∵PN=NB=8-t,
∴ON=OB-NB,
∴ON=12-(8-t)=4+t,
∴OH=4+t-2=2+t,
S1=
| 1 |
| 2 |
| 3 |
=2
| 3 |
| 3 |
∵2
| 3 |
∴S随t增大而增大,
当t=1时,S最大=8
| 3 |
当1<t<2时,如图4,S2=S五边形IFONG,
作GH⊥OB于H,
∵AP2=
| 3 |
∴AF=2
| 3 |
∴OF=4
| 3 |
| 3 |
∴EF=2
| 3 |
| 3 |
| 3 |
=2
| 3 |
| 3 |

∴EI=2t-2,
∴S2=S梯形EONG-S△EFI
=2
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
=-2
| 3 |
| 3 |
| 3 |
∵-2
| 3 |
∴当t=-
| b |
| 2a |
| 3 |
| 2 |
S2最大=
17
| ||
| 2 |
当t=2时,如图5,
MP=MN=6,
N与D重合,

S3=S梯形IMNG,
=
| ||
| 4 |
| ||
| 4 |
=8
| 3 |
∴S=
|
S最大=
17
| ||
| 2 |
(4)∵△ODR是等腰三角形,
①当D为顶点,OD=OR1=6时,
DR1=6-2
| 2 |
当D为顶点时,R1不存在,
此时R1不存在,使△ODR是等腰三角形,
②当R2为顶点,OR2=DR2时,
R2在EC的中点处,
∵AO=4
| 3 |

∴BO=12,
∵D为OB中点,
∴DO=EC=6,
∴ER2=3,
∵OB=12,∠B=30°,
∴OP2=6,
∴R2P2=3,
∴ER2=P2R2=3,
∴CP2=3
| 3 |
∴AP2=4
| 3 |
| 3 |
| 3 |
t2=
| ||
|
③当O为等腰三角形顶角的顶点时,
CR3=6-2
| 6 |
CP3=
6-2
| ||
| 2 |
| 3 |
| 3 |
| 2 |
AP3=4
| 3 |
| 3 |
| 2 |
=6
| 2 |
| 3 |
∴t3=
6
| ||||
|
| 6 |
综上所述:t=1时,△ODR是等腰三角形.
点评:此题主要考查了二次函数的综合应用以及相似三角形的性质等知识,(3)(4)小题中,都用到了分类讨论的数学思想,难点在于考虑问题要全面,做到不重不漏.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案
相关题目

 ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
 ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
 ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.