题目内容
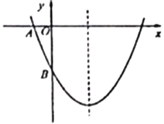
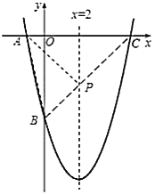
【题目】如图,已知二次函数![]() 的图像与坐标轴交于点
的图像与坐标轴交于点![]() 和点
和点![]() .
.
(1)求该二次函数的解析式;
(2)已知该函数图像的对称轴上存在一点![]() ,使得
,使得![]() 的周长最小.请求出点
的周长最小.请求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 是等腰三角形,请直接写出所有符合条件的点
是等腰三角形,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用待定系数法求解函数解析式即可;
(2)先求解抛物线与![]() 轴的另一个交点的坐标,由
轴的另一个交点的坐标,由![]() 两点关于关于对称轴对称,连接
两点关于关于对称轴对称,连接![]() 交对称轴与
交对称轴与![]() 点,则
点,则![]() 的周长最短,再求解
的周长最短,再求解![]() 的解析式即可得到答案;
的解析式即可得到答案;
(3)先求解![]() 的长度,分别以
的长度,分别以![]() 为圆心,
为圆心,![]() 为半径画弧,得到与
为半径画弧,得到与![]() 轴的交点符合题意,作
轴的交点符合题意,作![]() 的垂直平分线与
的垂直平分线与![]() 轴的交点也符合题意,从而可得答案.
轴的交点也符合题意,从而可得答案.
解:(1)根据题意,把点![]() 和点
和点![]() 代入函数解析式.得
代入函数解析式.得
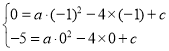 ,
,
解得![]() ,
,
∴二次函数的表达式为![]() ;
;
(2)令![]() ,得二次函数
,得二次函数![]() 的图象与
的图象与![]() 轴的另一个交点坐标
轴的另一个交点坐标![]() ;
;
由于![]() 是对称轴
是对称轴![]() 上一点,
上一点,
连接![]() ,由于
,由于![]() ,
,
要使![]() 的周长最小,只要
的周长最小,只要![]() 最小;
最小;
由于点![]() 与点
与点![]() 关于对称轴
关于对称轴![]() 对称,连接
对称,连接![]() 交对称轴于点
交对称轴于点![]() ,
,
则![]() ,根据两点之间,线段最短,可得
,根据两点之间,线段最短,可得![]() 的最小值为
的最小值为![]() ;
;
因而![]() 与对称轴
与对称轴![]() 的交点
的交点![]() 就是所求的点;
就是所求的点;
设直线![]() 的解析式为
的解析式为![]() ,
,
根据题意可得![]() 解得
解得![]()
所以直线![]() 的解析式为
的解析式为![]() ;
;
因此直线![]() 与对称轴
与对称轴![]() 的交点坐标是方程组
的交点坐标是方程组![]() 的解,解得
的解,解得![]() ,
,
所求的点![]() 的坐标为
的坐标为![]() ;
;
(3)![]()
![]()
以![]() 为圆心,
为圆心,![]() 为半径画弧,交
为半径画弧,交![]() 轴于
轴于![]()
![]()
![]()
![]()
以![]() 为圆心,
为圆心,![]() 为半径,交
为半径,交![]() 轴于
轴于![]()
由等腰三角形的三线合一得到:![]()
![]()
![]()
作![]() 的垂直平分线交
的垂直平分线交![]() 轴于
轴于![]()
设![]()
由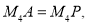
![]()
![]()
![]()
综上:![]() 或
或![]() 或
或![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某学校为了解九年级男同学1000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制了不完整的成绩等级频数表和扇形统计图.
成绩等级 | 频数 |
A | 24 |
B | 10 |
C | b |
D | 2 |
合计 | a |
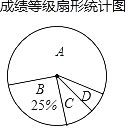
(1)表中a= ,b= ;
(2)扇形图中C的圆心角度数是 ;
(3)若该校共有九年级男生600人,请估计没有获得A等级的学生人数.