题目内容
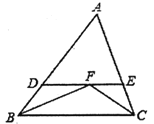
【题目】如图,Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连结AE,作AF⊥AE且AF=AE.
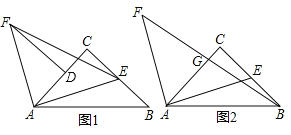
(1)如图1,过F点作FD⊥AC交AC于D点,求证:FD=BC;
(2)如图2,连结BF交AC于G点,若AG=3,CG=1,求证:E点为BC中点;
(3)当E点在射线CB上,连结BF与直线AC交于G点,若BC=4,BE=3,则![]() = (直接写出结果)
= (直接写出结果)
【答案】(1)见解析;(2)见解析;(3)![]() 或
或![]()
【解析】
(1)证明△AFD≌△EAC,根据全等三角形的性质得到DF=AC,等量代换证明结论;
(2)作FD⊥AC于D,证明△FDG≌△BCG,得到DG=CG,求出CE,CB的长,得到答案;
(3)过F作FD⊥AG的延长线交于点D,根据全等三角形的性质得到CG=GD,AD=CE=7,代入计算即可.
(1)∵FD⊥AC,
∴∠FDA=90°,
∴∠DFA+∠DAF=90°,
∠CAE+∠DAF=90°,
∴∠DFA=∠CAE,
在△AFD和△EAC中,
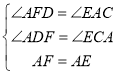 ,
,
∴△AFD≌△EAC(AAS),
∴DF=AC,
∵AC=BC,
∴FD=BC;
(2)作FD⊥AC于D,
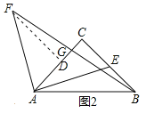
由(1)得,FD=AC=BC,AD=CE,
在△FDG和△BCG中,
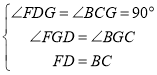 ,
,
∴△FDG≌△BCG(AAS),
∴DG=CG=1,
∴AD=2,
∴CE=2,
∵BC=AC=AG+CG=4,
∴E点为BC中点;
(3)当点E在CB的延长线上时,过F作FD⊥AG的延长线交于点D,
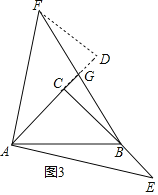
BC=AC=4,CE=CB+BE=7,
由(1)(2)知:△ADF≌△ECA,△GDF≌△GCB,
∴CG=GD,AD=CE=7,
∴![]() ,
,
∴![]() ,
,
当点E在线段BC上时,过F作FD⊥AG的延长线交于点D,
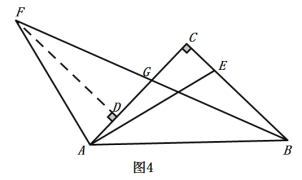
BC=AC=4,CE=CB-BE=1,
由(1)(2)知:△ADF≌△ECA,△GDF≌△GCB,
∴CG=GD,AD=CE=1,
∴![]() ,
,
∴![]() ,
,
故答案为:![]() 或
或![]() .
.

【题目】甲、乙两班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如表,请根据表中数据解答下列问题
进球数/个 | 10 | 9 | 8 | 7 | 6 | 5 |
甲 | 1 | 1 | 1 | 4 | 0 | 3 |
乙 | 0 | 1 | 2 | 5 | 0 | 2 |
(1)分别写出甲、乙两班选手进球数的平均数、中位数与众数;
(2)如果要从这两个班中选出一个班级参加学校的投篮比赛,争取夺得总进球团体的第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?