题目内容
【题目】已知四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:①AB∥CD;②OA=OC;③AB=CD;④∠BAD=∠DCB;⑤AD∥BC,
从以上5个条件中任选2个条件为一组,能判定四边形ABCD是平行四边形的有( )组.

A. 4 B. 5 C. 6 D. 7
【答案】C
【解析】分析:根据平行四边形的判定来进行选择.①两组对边分别平行的四边形是平行四边形;②两组对角分别平行的四边形是平行四边形;③两组对边分别相等的四边形是平行四边形;④一组对边平行且相等的四边形是平行四边形;⑤对角线互相平分的四边形是平行四边形.
详解:共有6组可能:①②;①③;①④;①⑤;②⑤;④⑤.
选择①与②:∵AB∥CD,
∴∠BAO=∠DCO,∠ABO=∠CDO,
在△AOB与△COD中,
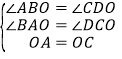 ,
,
∴△AOB≌△COD,
∴AB=CD,
∴四边形ABCD为平行四边形.
①与③(根据一组对边平行且相等)
①与④:∵∠BAD=∠DCB
∴AD∥BC
又AB∥DC
根据两组对边分别平行可推出四边形ABCD为平行四边形.
①与⑤,根据定义,两组对边分别平行的四边形是平行四边形;
②与⑤:∵AD∥BC
OA=OC
∴△AOD≌△COB
故AD=BC,四边形ABCD为平行四边形.
④与⑤:根据两组对边分别平行可推出四边形ABCD为平行四边形.
共有6种可能.
故选:C.

练习册系列答案
相关题目