题目内容
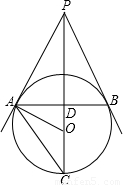
如图,PA、PB是⊙O的两条切线,其切点分别为A、B,PO交AB于点D,PO的延长线交⊙O于点C,根据图形给出下面四个结论:①∠PAB=∠PCA;②PA2=PD•PC;③∠PAB=∠PBA;④∠AOD=2∠ACO.其中错误的结论的个数为( )
A.1
B.2
C.3
D.4
【答案】分析:由PA与PB为圆O的两条切线,根据切线长定理得到PA=PB,利用等边对等角得到∠PAB=∠PBA,选项③正确;连接BC,利用弦切角等于夹弧所对的圆周角得到得到∠PAB=∠ACB,故∠PAB不等于∠PCA,选项①错误;由PA为圆O的切线,PC为圆O的割线,利用切割线定理得到关系式,即可对②作出判断;由同弧所对的圆心角等于所对圆周角的2倍,得到∠AOD=2∠ACO,选项④正确,即可得出错误选项的个数.
解答: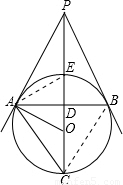 解:∵PA、PB是⊙O的两条切线,
解:∵PA、PB是⊙O的两条切线,
∴PA=PB,
∴∠PAB=∠PBA,故选项③正确;
连接BC,AE,可得出∠PAB=∠ACB,
∴∠PAB≠∠PCA,故选项①错误;
∵PA为⊙O的切线,PC为⊙O的割线,
∴∠PAE=∠PCA,
又∵∠APE=∠CPA,
∴△APE∽△CPA,
∴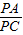 =
=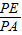 ,即PA2=PE•PC,故选项②错误;
,即PA2=PE•PC,故选项②错误;
∵∠AOD与∠ACO都对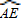 ,
,
∴∠AOD=2∠ACO,故选项④正确.
则错误的个数有2个.
故选B.
点评:此题考查了切线的性质,切割线定理,等边对等角,圆周角定理,以及相似三角形的判定与性质,熟练掌握切线的性质是解本题的关键.
解答:
 解:∵PA、PB是⊙O的两条切线,
解:∵PA、PB是⊙O的两条切线,∴PA=PB,
∴∠PAB=∠PBA,故选项③正确;
连接BC,AE,可得出∠PAB=∠ACB,
∴∠PAB≠∠PCA,故选项①错误;
∵PA为⊙O的切线,PC为⊙O的割线,
∴∠PAE=∠PCA,
又∵∠APE=∠CPA,
∴△APE∽△CPA,
∴
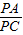 =
=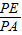 ,即PA2=PE•PC,故选项②错误;
,即PA2=PE•PC,故选项②错误;∵∠AOD与∠ACO都对
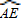 ,
,∴∠AOD=2∠ACO,故选项④正确.
则错误的个数有2个.
故选B.
点评:此题考查了切线的性质,切割线定理,等边对等角,圆周角定理,以及相似三角形的判定与性质,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
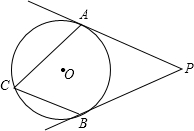 如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
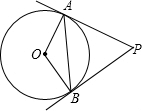 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度. 4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
 (2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于
(2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于