题目内容
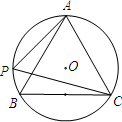 如图,A,P,B,C是⊙O上的四点,且满足∠BAC=∠APC=60°,
如图,A,P,B,C是⊙O上的四点,且满足∠BAC=∠APC=60°,(1)请判断△ABC的形状,并说明理由.
(2)若⊙O半径为7,AP=6,求圆心O到AP的距离.
分析:(1)由∠BAC=∠APC=60°,根据圆周角定理,可求得△ABC的各内角的度数,继而证得△ABC是等边三角形;
(2)首先过O作OD⊥AP,垂足为D,连接OA,易求得AP与AD的长,又由勾股定理,求得答案.
(2)首先过O作OD⊥AP,垂足为D,连接OA,易求得AP与AD的长,又由勾股定理,求得答案.
解答:解:(1)△ABC是等边三角形,
理由如下:在△ABC中,
∵∠B=∠APC,且∠APC=60°,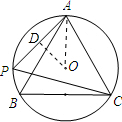
∴∠B=60°,
又∵∠BAC=60°,
∴∠ACB=180°-∠BAC-∠ABC=180°-60°-60°=60°,
∴△ABC是等边三角形;
(2)过O作OD⊥AP,垂足为D,连接OA,
∴AD=
AP,∠ADO=90°,
∵AP=6,
∴AD=3,
∴在R t△ADO中OD=
=
=2
,
∴圆心O到AP距离为2
.
理由如下:在△ABC中,
∵∠B=∠APC,且∠APC=60°,

∴∠B=60°,
又∵∠BAC=60°,
∴∠ACB=180°-∠BAC-∠ABC=180°-60°-60°=60°,
∴△ABC是等边三角形;
(2)过O作OD⊥AP,垂足为D,连接OA,
∴AD=
| 1 |
| 2 |
∵AP=6,
∴AD=3,
∴在R t△ADO中OD=
| AO2-AD2 |
| 72-32 |
| 10 |
∴圆心O到AP距离为2
| 10 |
点评:此题考查了圆周角定理、等边三角形的判定与性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
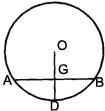 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=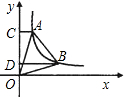 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

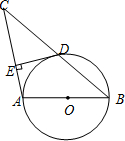 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.