题目内容
【题目】如图，直线 PQ 上有一点 O，点 A 为直线外一点，连接 OA，在直线 PQ 上找一点 B，使得△AOB 是等腰三角形，这样的点 B 有_____个.
【答案】4或2
【解析】
①当AO不垂直于PQ时，若OA=OB时点B有2个；若OA=AB时点B有1个,；若OB=AB时点B有1个.
②当AO⊥PQ时，只有OA=OB时点B有2个.
①AO不垂直于PQ，分以下三种情况：
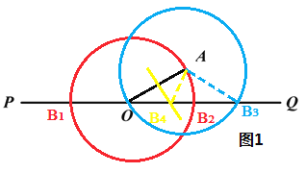
当OA=OB时，以点O为圆心，OA为半径的圆与直线PQ的交点即为所求的点B，有2个(见图1上B1、B2)；
当OA=AB时，以点A为圆心，OA为半径的圆与直线PQ的交点即为所求的点B，其中一点与O点重合，有效点有1个, (见图1上B3)；
当OB=AB时，作OA的垂直平分线与直线PQ的交点即为所求的点B，有1个(见图1上B4).
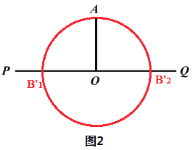
②当AO⊥PQ时，AB为直角边，所以两个直角边相等才能是等腰三角形，即只有OA=OB一种可能，点B有2个(见图2上B'1、B'2)
故填4或2.
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
