题目内容
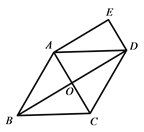
【题目】已知：如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD．
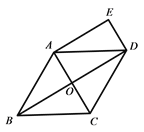
求证：四边形AODE是矩形；（2）若AB＝6，∠BCD＝120°，求四边形AODE的面积．
【答案】（1）见解析（2）9
【解析】试题分析：
（1）由已知易得四边形AODE是平行四边形，由四边形ABCD是菱形可得AC⊥BD，从而可得∠AOD=90°，由此可得平行四边形AODE是矩形；
（2）由四边形ABCD是菱形，∠BCD=120°易证△ABC是等边三角形，从而可得AC=AB=6，AO=3，结合AC⊥BD由勾股定理可得BO=3，则OD=3，由此可得矩形AODE的面积为
.
试题解析：
（1）∵DE∥AC，AE∥BD，
∴四边形AODE是平行四边形，
∵在菱形ABCD中，AC⊥BD，
∴平行四边形AODE是矩形，
（2）∵∠BCD=120°，AB∥CD，
∴∠ABC=180°﹣120°=60°，
∵AB=BC，
∴△ABC是等边三角形，
∴OA=
×4=2，
∵在菱形ABCD中，AC⊥BD，
∴由勾股定理OB=3，
∵四边形ABCD是菱形，
∴OD=OB=3，
∴四边形AODE的面积=OAOD=9．
练习册系列答案
相关题目
【题目】在某市2016年“书香校园，经典诵读”比赛活动中，有32万名学生参加比赛活动，其中有8万名学生分别获得一、二、三等奖，从获奖学生中随机抽取部分，绘制成不完整的统计表（如表），请根据图表解答下列问题．
获奖等级 | 频数 |
一等奖 | a |
二等奖 | b |
三等奖 | 275 |
（1）表格中a的值为 ， b的值为 ．
（2）扇形统计图中表示获得一等奖的扇形的圆心角为度．
（3）估计全市有多少名学生获得三等奖？
