题目内容
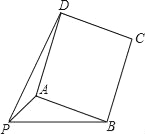
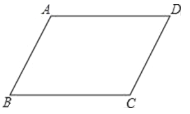
【题目】在一次数学活动中,黑板上画着如图所示的图形,活动前老师在准备的四张卡片(大小、颜色、形状相同)的正面上分别写有如下四个等式中的一个等式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;小英同学闭上眼睛从四张卡片中随机抽出一张,再从剩下的卡片中随机抽出另一张,请结合图形回答下列问题:
;小英同学闭上眼睛从四张卡片中随机抽出一张,再从剩下的卡片中随机抽出另一张,请结合图形回答下列问题:
(1)当抽得②和④时,用②和④作条件能否判定四边形是平行四边形,请说明理由;
(2)请你用树状图或表格表示抽取两张卡片上的条件的所有可能出现的结果(用序号表示)并求以已经抽取的两张卡片上的条件为已知,使四边形不能构成平行四边形的概率.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由AD//BC可得∠A与∠B互补,再根据∠A=∠C,可得到∠B与∠C互补,继而可得AB//CD,进而根据平行四边形的定义证明即可;
(2)画树状图得到所有可能的情况,然后找出符合题意的条件数,利用概率公式求解即可.
(1)用②![]() 和④
和④![]() 作条件,能判定四边形是平行四边形,
作条件,能判定四边形是平行四边形,
理由:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形;
是平行四边形;
(3)抽取两张卡片上的等式的所有可能出现的结果为:

其中,含①③,②③,②④,③④的组合都能构成平行四边形,
∴使四边形不能构成平行四边形的概率=![]() .
.

练习册系列答案
相关题目