Question

【题目】在平面直角坐标系中，点A的坐标是（1，3），将点A绕原点O顺时针旋转90°得到点A′，则点A′的坐标是（ ）

A. （－3，1） B. （3，－1） C. （－1，3） D. （1，－3）

Answer 1

【答案】B

【解析】

如图，过点A作AB⊥x轴于点B，过点A′作A′C⊥x轴于点C，根据旋转的性质得出∠AOA′=90°，AO=A′O，根据同角的余角相等得出∠A′OC=∠AOB，然后根据AAS判断出△A′OC≌△AOB，根据全等三角形对应边相等得出OC=OB=1，A′C=AB=3，从而根据点所在的象限得出坐标.

如图，过点A作AB⊥x轴于点B，过点A′作A′C⊥x轴于点C，

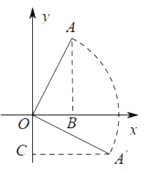
∴∠ABO=∠A′CO=90°，

∵点A′是由点A绕点O顺时针旋转90°得到的，

∴∠AOA′=90°，AO=A′O，

∴∠A′OC+∠A′OB=90°，∠A′OB+∠AOB=90°，

∴∠A′OC=∠AOB，

∴△A′OC≌△AOB，

∴OC=OB，A′C=AB，

∵点A的坐标为（1，3），

∴OC=OB=1，A′C=AB=3，

又点A′在第四象限，

∴点A′的坐标为（3，-1），

故选B.