题目内容
【题目】“8字”的性质及应用:
(1)如图1,AD、BC相交于点O,得到一个“8字”ABCD,求证:∠A+∠B=∠C+∠D.
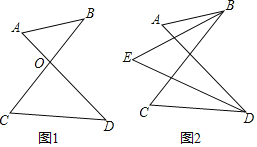
(2)如图2,∠ABC和∠ADC的平分线相交于点E,利用(1)中的结论证明:∠E=![]() (∠A+∠C).
(∠A+∠C).
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据三角形的内角和定理和对顶角相等即可证∠A+∠B=∠C+∠D;
(2)根据角平分线的定义可得:∠ABE=∠EBC,∠CDE=∠EDA,再根据(1)中结论列出两个等式,将两个等式相加即可证出∠E=![]() (∠A+∠C).
(∠A+∠C).
证明:(1)∵∠A+∠B=180°-∠AOB,∠C+∠D=180°-∠COD,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)∵∠ABC和∠ADC的平分线相交于点E,
∴∠ABE=∠EBC,∠CDE=∠EDA,
由(1)的结论可知:∠A+∠ABE=∠E+∠EDA①,∠C+∠CDE=∠E+∠EBC②,
①+②得:∠A+∠ABE+∠C+∠CDE=∠E+∠EDA+∠E+∠EBC,
∴∠A+∠C=2∠E,
∴∠E=![]() (∠A+∠C).
(∠A+∠C).

练习册系列答案
相关题目






