题目内容
如图，在等腰△ABC中，AC=BC，AC的垂直平分线DE交BC于点D，交AC于点E，△ABD的周长为10，BC=6，则△ABC的周长为
- A.4
- B.10
- C.12
- D.16
D
分析：根据线段垂直平分线的性质得到DA=DC，由△ABD的周长为10得AB+AD+BD=10，则AB+DC+BD=10，即AB+BC=10，而CA=CB，BC=6，即可得到△ABC的周长．
解答：∵AC的垂直平分线DE交BC于点D，
∴DA=DC，
又∵△ABD的周长为10，即AB+AD+BD=10，
∴AB+DC+BD=10，
∴AB+BC=10，
而CA=CB，BC=6，
∴CA=6，
∴△ABC的周长=AB+BC+AC=10+6=16．
故选D．
点评：本题考查了线段垂直平分线的性质：线段垂直平分线上的点到线段两段点的距离相等．也考查了三角形周长的定义．
分析：根据线段垂直平分线的性质得到DA=DC，由△ABD的周长为10得AB+AD+BD=10，则AB+DC+BD=10，即AB+BC=10，而CA=CB，BC=6，即可得到△ABC的周长．
解答：∵AC的垂直平分线DE交BC于点D，
∴DA=DC，
又∵△ABD的周长为10，即AB+AD+BD=10，
∴AB+DC+BD=10，
∴AB+BC=10，
而CA=CB，BC=6，
∴CA=6，
∴△ABC的周长=AB+BC+AC=10+6=16．
故选D．
点评：本题考查了线段垂直平分线的性质：线段垂直平分线上的点到线段两段点的距离相等．也考查了三角形周长的定义．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
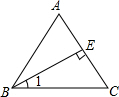如图，在等腰△ABC中，AB=AC，BE⊥AC，垂足为E，则∠1与∠A的关系式为（ ）| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
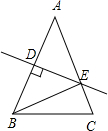如图，在等腰△ABC中，AB=AC，AB的垂直平分线DE交AB于点D，交另一腰AC于点E，若∠EBC=15°，则∠A=
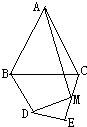24、如图，在等腰△ABC中，AB=AC，∠ABC=α，在四边形BDEC中，DB=DE，∠BDE=2α，M为CE的中点，连接AM，DM．
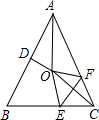（2012•丽水）如图，在等腰△ABC中，AB=AC，∠BAC=50°．∠BAC的平分线与AB的中垂线交于点O，点C沿EF折叠后与点O重合，则∠CEF的度数是
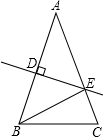如图，在等腰△ABC中，AB=AC=10cm，直线DE垂直平分AB，分别交AB、AC于D、E两点．若BC=8cm，则△BCE的周长是