题目内容
【题目】如图,已知AB∥CD,点P在直线BD上(点P与点B、D不重合),分别记∠BAP,∠DCP,∠APC为∠1,∠2,∠3.
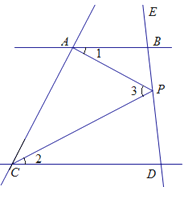
(1)当点P在B、D两点间移动时,写出∠1,∠2,∠3之间的等量关系,并说明理由;
(2)当点P在射线BE上移动时,(1)中的等量关系还存在吗?若存在,请说明理由;若不存在,请写出一个你认为正确的等量关系,并说明理由。
【答案】(1)等量关系:∠3=∠1+∠2,(2)(1)中等量关系不存在了.
【解析】(1)首先过点P作PQ∥AB,由于AB∥CD,可得PQ∥CD,然后由两直线平行,同位角相等,求得答案;(2)由题意画出图形得知,(1)中的等量关系不存在了.
解:(1)等量关系:∠3=∠1+∠2,
作PQ∥AB,
∵AB∥CD,∴PQ∥CD,
∴∠APQ=∠1,∠CPQ=∠2,
∴∠3=∠APQ +∠CPQ=∠1+∠2
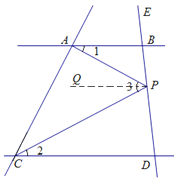
(2)答:(1)中等量关系不存在了.
如图所示

AB∥CD
∴ ∠1= ∠PCD
∴∠2+∠1=180°
∠2+∠APC+∠PAB=180°
∴∠PCD=∠1=∠APC+∠PAB
“点睛”本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.合理添加平行线是解决此题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目