题目内容
【题目】在平面直角坐标系xOy中,已知定点A(1,0)和B(0,1).

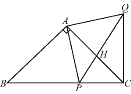
(1)如图1,若动点C在x轴上运动,则使△ABC为等腰三角形的点C有几个?
(2)如图2,过点A,B向过原点的直线l作垂线,垂足分别为M、N,试判断线段AM、BN、MN之间的数量关系,并说明理由.
【答案】(1)4个;(2)AM+BN=MN;理由见解析.
【解析】
(1)如图,当以AB为腰时,有3个;当以AB为底时,有1个;
(2)通过“角角边”证明△AOM≌△OBN,得到AM=ON,OM=BN,则可得到AM+BN=MN.
解:(1)如图, 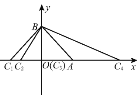
当以AB为腰时,有3个;当以AB为底时,有1个,
∴使△ABC为等腰三角形的点C有4个;
(2)AM+BN=MN.
理由:由已知可得OA=OB,∠AOM=90°-∠BON=∠OBN,
在△AOM和△OBN中,
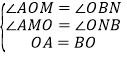 ,
,
∴△AOM≌△OBN(AAS),
∴AM=ON,OM=BN,
∴AM+BN=ON+OM=MN.

练习册系列答案
相关题目
【题目】去年6月某日自治区部分市、县的最高气温(℃)如下表:
区县 | 吐鲁番 | 塔城 | 和田 | 伊宁 | 库尔勒 | 阿克苏 | 昌吉 | 呼图壁 | 鄯善 | 哈密 |
气温(℃) | 33 | 32 | 32 | 30 | 30 | 29 | 29 | 31 | 30 | 28 |
则这10个市、县该日最高气温的众数和中位数分别是( )
A.32,32
B.32,30
C.30,30
D.30,32