题目内容
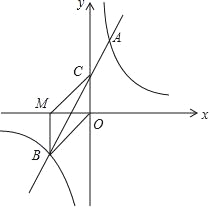
【题目】如图，在平面直角坐标系中，一次函数y=mx+n（m≠0）的图象与反比例函数y=
（k≠0）的图象交于第一、三象限内的A、B两点，与y轴交于点C，过点B作BM⊥x轴，垂足为M，BM=OM，OB=2
，点A的纵坐标为4．
（1）求该反比例函数和一次函数的解析式；
（2）连接MC，求四边形MBOC的面积．
【答案】（1）y=2x+2；（2）4
【解析】试题分析：（1）根据题意可以求得点B的坐标，从而可以求得反比例函数的解析式，进而求得点A的坐标，从而可以求得一次函数的解析式；
（2）根据（1）中的函数解析式可以求得点C，点M、点B、点O的坐标，从而可以求得四边形MBOC的面积．
试题解析：（1）由题意可得，BM=OM，OB=
，∴BM=OM=2，∴点B的坐标为（﹣2，﹣2），设反比例函数的解析式为
，则﹣2=
，得k=4，∴反比例函数的解析式为
，∵点A的纵坐标是4，∴4=
，得x=1，∴点A的坐标为（1，4），∵一次函数y=mx+n（m≠0）的图象过点A（1，4）、点B（﹣2，﹣2），∴
，得：
，即一次函数的解析式为y=2x+2；
（2）∵y=2x+2与y轴交与点C，∴点C的坐标为（0，2），∵点B（﹣2，﹣2），点M（﹣2，0），点O（0，0），∴OM=2，OC=2，MB=2，∴四边形MBOC的面积是：
OMON+OMMB =×2×2+×2×2=4．
口算题卡加应用题集训系列答案
【题目】学生小明、小华为了解本校八年级学生每周上网的时间，各自进行了抽样调查．小明调查了八年级信息技术兴趣小组中40名学生每周上网的时间，算得这些学生平均每周上网时间为2.5h；小华从全体320名八年级学生名单中随机抽取了40名学生，调查了他们每周上网的时间，算得这些学生平均每周上网时间为1.2h．小明与小华整理各自样本数据，如表所示．
时间段（h/周） | 小明抽样人数 | 小华抽样人数 |
0～1 | 6 | 22 |
1～2 | 10 | 10 |
2～3 | 16 | 6 |
3～4 | 8 | 2 |
（每组可含最低值，不含最高值）
请根据上述信息，回答下列问题：
（1）你认为哪位学生抽取的样本具有代表性？_____．
估计该校全体八年级学生平均每周上网时间为_____h；
（2）在具有代表性的样本中，中位数所在的时间段是_____h/周；
（3）专家建议每周上网2h以上（含2h）的同学应适当减少上网的时间，根据具有代表性的样本估计，该校全体八年级学生中有多少名学生应适当减少上网的时间？
