题目内容
已知反比例函数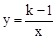 图象的两个分支分别位于第一、第三象限.
图象的两个分支分别位于第一、第三象限.
(1)求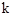 的取值范围;
的取值范围;
(2)若一次函数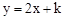 的图象与该反比例函数的图象有一个交点的纵坐标是4.
的图象与该反比例函数的图象有一个交点的纵坐标是4.
①求当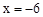 时反比例函数
时反比例函数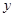 的值;
的值;
②当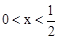 时,求此时一次函数
时,求此时一次函数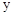 的取值范围.
的取值范围.
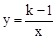 图象的两个分支分别位于第一、第三象限.
图象的两个分支分别位于第一、第三象限.(1)求
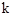 的取值范围;
的取值范围;(2)若一次函数
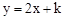 的图象与该反比例函数的图象有一个交点的纵坐标是4.
的图象与该反比例函数的图象有一个交点的纵坐标是4.①求当
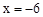 时反比例函数
时反比例函数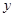 的值;
的值;②当
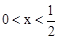 时,求此时一次函数
时,求此时一次函数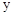 的取值范围.
的取值范围.解:(1)∵反比例函数图象两支分别位于第一、三象限,
∴k-1>0,解得:k>1。
(2)①∵一次函数与反比例函数交点纵坐标为4,
∴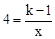 ,
,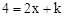
联立之,得: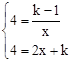 ,解得k=3。
,解得k=3。
∴反比例解析式为 。
。
当x=-6时,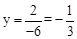 。
。
②由k=3,得到一次函数解析式为y=2x+3,即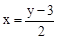 。
。
∵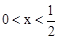 ,∴
,∴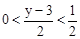 ,解得:3<y<4。
,解得:3<y<4。
∴一次函数y的取值范围是3<y<4。
∴k-1>0,解得:k>1。
(2)①∵一次函数与反比例函数交点纵坐标为4,
∴
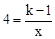 ,
,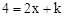
联立之,得:
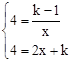 ,解得k=3。
,解得k=3。∴反比例解析式为
 。
。当x=-6时,
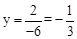 。
。②由k=3,得到一次函数解析式为y=2x+3,即
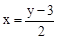 。
。∵
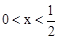 ,∴
,∴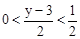 ,解得:3<y<4。
,解得:3<y<4。∴一次函数y的取值范围是3<y<4。
反比例函数与一次函数的交点问题,反比例函数的性质,曲线上点的坐标与方程的关系,解方程组和不等式。
【分析】(1)由反比例函数图象过第一、三象限,得到反比例系数k-1大于0,列出关于k的不等式,求出不等式的解集得到k的范围。
(2)①由一次函数与反比例函数交点纵坐标为4,将y=4代入一次函数及反比例函数解析式,联立求解即可得到k的值,确定出反比例函数解析式,然后将x=-6代入求出的反比例函数解析式中即可求出对应的函数值y的值。
②将求出的k值代入一次函数解析式中,确定出解析式,应y表示出x,根据x的范围列出关于y的不等式,求出不等式的解集即可得到y的取值范围。
【分析】(1)由反比例函数图象过第一、三象限,得到反比例系数k-1大于0,列出关于k的不等式,求出不等式的解集得到k的范围。
(2)①由一次函数与反比例函数交点纵坐标为4,将y=4代入一次函数及反比例函数解析式,联立求解即可得到k的值,确定出反比例函数解析式,然后将x=-6代入求出的反比例函数解析式中即可求出对应的函数值y的值。
②将求出的k值代入一次函数解析式中,确定出解析式,应y表示出x,根据x的范围列出关于y的不等式,求出不等式的解集即可得到y的取值范围。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (
( ,
, )的图象经过点
)的图象经过点 (1,2),
(1,2), (
( ,
, )(
)( ),过点B作
),过点B作 轴的垂线,垂足为C.
轴的垂线,垂足为C.
 时,求点B的坐标;
时,求点B的坐标; 的值随
的值随 的增大而增大。请你写出满足以上条件的一个函数关系式 。
的增大而增大。请你写出满足以上条件的一个函数关系式 。 ,下列说法不正确的是( )
,下列说法不正确的是( ) 时,
时, 随
随 的增大而增大
的增大而增大 时,
时, 与体积
与体积
 之间的函数关系如图所示。
之间的函数关系如图所示。
 与
与 时,二氧化碳的密度
时,二氧化碳的密度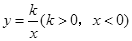 的图象上.若
的图象上.若
 ,点B在双曲线
,点B在双曲线 上,点C在直线y=x上,则k的值为____________.
上,点C在直线y=x上,则k的值为____________.
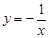 的图象上有两点
的图象上有两点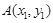 、
、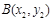 ,且
,且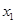 <
<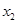 ,那么下列结论正确的
,那么下列结论正确的 <
<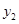
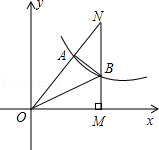
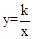 经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为5,则k的值是 ▲ .
经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为5,则k的值是 ▲ .