ЬтФПФкШн
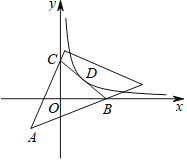
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпyЃНax2+bx+3ОЙ§ЕуA(Љ3ЃЌ0)ЃЌB(Љ1ЃЌ0)СНЕуЃЌХзЮяЯпЕФЖЅЕуЮЊMЃЌжБЯпyЃНЉ4x+9гыyжсНЛгкЕуCЃЌгыжБЯпOMНЛгкЕуDЃЎ
(1)ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
(2)Й§Q(0ЃЌ3)зїВЛЦНаагкxжсЕФжБЯпl
ЂйШчЭМ2ЃЌНЋХзЮяЯпЦНвЦЃЌЕБЖЅЕужСдЕуЪБЃЌжБЯпlНЛХзЮяЯпгкЕуEЁЂFЃЌдкyжсЩЯДцдквЛЕуPЃЌЪЙЁїPEFЕФФкаФдкyжсЩЯЃЌЧѓЕуPЕФзјБъЃЛ
ЂкжБЯпlНЛЁїCMDЕФБпCMЁЂCDгкЕуGЁЂH(GЕуВЛгыMЕужиКЯЁЂHЕуВЛгыDЕужиКЯ)ЃЎSЫФБпаЮMDHGЃЌSЁїCGHЗжБ№БэЪОЫФБпаЮMDHGКЭЁїCGHЕФУцЛ§ЃЌЪдЬНОП![]() ЕФзюДѓжЕЃЎ
ЕФзюДѓжЕЃЎ
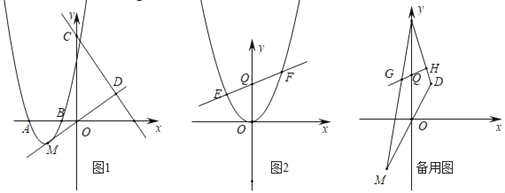
ЁОД№АИЁП(1)ХзЮяЯпЕФНтЮіЪНЮЊyЃНx2+4x+3ЃЛ(2)ЂйЕуPзјБъЮЊ(0ЃЌЉ3)ЃЛЂкЕБxЃН![]() ЪБЃЌ
ЪБЃЌ ![]() газюДѓжЕЃЌзюДѓжЕЮЊ
газюДѓжЕЃЌзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉНЋAЃЈ3ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉДњШыХзЮяЯпНтЮіЪНЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЂйЗжБ№аДГіХзЮяЯпЦНвЦКѓЕФНтЮіЪНКЭжБЯпEFЕФНтЮіЪНЃЌЙ§PзїGHЁЮxжсЃЌЗжБ№Й§EЃЌFзїGHЕФДЙЯпЃЌДЙзуЗжБ№ЮЊGЃЌHЃЎгЩФкаФЕФаджЪЕУНЧЕШЃЌдйРћгУЯрЫЦШ§НЧаЮЕФаджЪПЩНтЃЛ
ЂкСЌНгOGЃЌгЩЕуCКЭЕуQЕФзјБъЃЌЕУCQЕШгк2OQЃЌгЩЕуMКЭЕуDзјБъЃЌЕУMOЕШгкODЃЌЗжБ№гУШ§НЧаЮGQOЕФУцЛ§БэЪОГіШ§НЧаЮCGQКЭШ§НЧаЮCGOЕФУцЛ§ЃЌ
дйЩшCGЃН1ЃЌMGЃНxЃЌгУКЌxЕФЪНзгБэЪОГіЯрЙиШ§НЧаЮКЭЫФБпаЮMDHGЕФУцЛ§ЃЌзюКѓНЋвЊЧѓЕФБШжЕзЊЛЏЮЊЙигкxЕФЖўДЮКЏЪ§ЃЌДгЖјПЩНтЃЎ
(1)ЁпХзЮяЯпyЃНax2+bx+3ОЙ§ЕуA(Љ3ЃЌ0)ЃЌB(Љ1ЃЌ0)СНЕуЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃНx2+4x+3ЃЎ
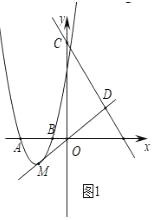
(2)ЂйНЋХзЮяЯпЦНвЦЃЌЕБЖЅЕужСдЕуЪБЃЌЦфНтЮіЪНЮЊyЃНx2ЃЌ
гЩEFЙ§Еу(0ЃЌ3)ЃЌЙЪЩшЦфНтЮіЪНЮЊyЃНkx+3(kЁй0)ЃЎ
ЩшТњзуЬѕМўЕиЕуPзјБъЮЊ(0ЃЌt)ЃЌ
ШчЭМЃЌЙ§PзїGHЁЮxжсЃЌЗжБ№Й§EЃЌFзїGHЕФДЙЯпЃЌДЙзуЗжБ№ЮЊGЃЌHЃЎ
ЁпЁїPEFЕФФкаФдкyжсЩЯЃЌ
ЁрЁЯGEPЃНЁЯEPQЃНЁЯQPFЃНЁЯHFPЃЌ
ЁрЁїGEPЁзЁїHFPЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр2![]() xFЃН(tЉ3)(xE+xF)ЃЌ
xFЃН(tЉ3)(xE+xF)ЃЌ
гЩyЃНx2ЃЌyЃНЉkx+3ЕУx2ЉkxЉ3ЃН0ЃЌ
ЁрxE+xFЃНkЃЌxExFЃНЉ3ЃЌ
Ёр2k(Љ3)ЃН(tЉ3)k
ЁпkЁй0ЃЌЁрtЃНЉ3ЃЌ
ЁрЕуPзјБъЮЊ(0ЃЌЉ3)ЃЎ

ЂкШчЭМЃЌСЌНгOGЃЌ
ЁпC(0ЃЌ9)Q(0ЃЌ3)ЃЌ
ЁрCQЃН2OQЃЌ
гжЁпM(Љ2ЃЌЉ1)ЃЌD(2ЃЌ1)ЃЌ
ЁрMOЃНODЃЎ
ЩшSЁїGQOЃНSЃЌ
ЁрSЁїCGQЃН2SЃЌSЁїCGOЃН3SЃЎ
ВЛЗСЩшCGЃН1ЃЌMGЃНxЃЌдђSЁїMGOЃН3xSЃЌ
ЁрSЁїCMOЃНSЁїCQO+SЁїMGOЃН3S+3xSЃН(3x+3)SЃЌ
ЁрSЁїCMDЃН2SЁїCMOЃН(6x+6)SЃЌ
ЩшQHЃНkQGЃЌгЩSЁїCGQЃН2SЃЌЕУSЁїCQHЃН2kSЃЌ
ЁрSЁїCGHЃН(2k+2)SЃЎ
ЁрSЫФБпаЮMDHGЃН(6x+6)SЉ(2k+2)SЃН(6xЉ2k+4)SЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌЂй
ЃЌЂй
Й§ЕуQзїQKЁЮMDЃЌНЛCDгкЕуKЃЌЙ§ЕуGзїGNЁЮMDЃЌНЛCDгкЕуNЃЌдђQKЁЮGNЃЎ
Ёр![]() ЃЌ
ЃЌ
ЁрQKЃН![]() ODЃН
ODЃН![]() MDЃЛ
MDЃЛ
ЁпGNЁЮMDЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
ЁпQKЁЮGNЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрkЃН![]() ЃЌ
ЃЌ
ДњШыЂйЪНЕУЃК![]() ЃН
ЃН![]() ЃН
ЃН ЃНЉx2+x+1ЃН
ЃНЉx2+x+1ЃН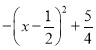 ЃЌ
ЃЌ
ЁрЕБxЃН![]() ЪБЃЌ
ЪБЃЌ ![]() газюДѓжЕЃЌзюДѓжЕЮЊ
газюДѓжЕЃЌзюДѓжЕЮЊ![]() ЃЎ
ЃЎ


 ПЦбЇЪЕбщЛюЖЏВсЯЕСаД№АИ
ПЦбЇЪЕбщЛюЖЏВсЯЕСаД№АИ