��Ŀ����
С����һ�θ߶���������У���ɽ���µ�O����һ������ɽ���ϵ���A���ȥ����ķ���·��Ϊ������. ��������ǿ���������������е�ˮƽ����Ϊ9��ʱ����ﵽ���ˮƽ�߶�Ϊ12�ף���֪ɽ��OA��ˮƽ����ļн�Ϊ30o��O��A�������  �ף�����������������ƽ��ֱ������ϵ̽���������⣺
�ף�����������������ƽ��ֱ������ϵ̽���������⣺

��1�������A�����ꣻ
��2���ж�С����һ���ܷ�Ѹ߶������O��ֱ�Ӵ�����A�㣬��˵�����ɣ�
 �ף�����������������ƽ��ֱ������ϵ̽���������⣺
�ף�����������������ƽ��ֱ������ϵ̽���������⣺
��1�������A�����ꣻ
��2���ж�С����һ���ܷ�Ѹ߶������O��ֱ�Ӵ�����A�㣬��˵�����ɣ�
�⣺��1�������⣬������ϵ�л�����ͼ
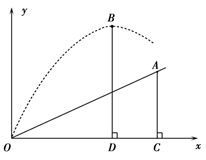
��Rt��AOC��
�ߡ�AOC =30 o ��OA=8 ��
��
��AC = OA=8 ��
��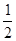 =
=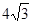 ��
��
��OC =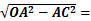 12��
12��
���A��������12��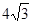 ����
����
��2���������֪�������ߵĶ���B�������ǣ�9��12��,
�������ߵĽ���ʽΪy=a(x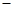 9)
9)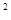 +12��
+12��
�������߹���O��0��0�����ѵ�O������������ʽ�еã�
0=a��0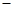 9��
9��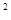 +12�����a =
+12�����a =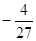 ��
��
�������ߵĽ���ʽΪy=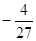 (x
(x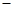 9)
9)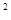 +12
+12
��x=12ʱ��y =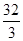
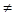
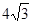 ��
��
��С����һ�˲��ܰѸ߶������O��ֱ�Ӵ�����A�㣮

��Rt��AOC��
�ߡ�AOC =30 o ��OA=8
 ��
����AC = OA=8
 ��
��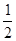 =
=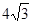 ��
����OC =
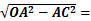 12��
12�����A��������12��
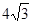 ����
������2���������֪�������ߵĶ���B�������ǣ�9��12��,
�������ߵĽ���ʽΪy=a(x
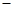 9)
9)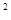 +12��
+12���������߹���O��0��0�����ѵ�O������������ʽ�еã�
0=a��0
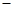 9��
9��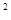 +12�����a =
+12�����a =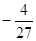 ��
���������ߵĽ���ʽΪy=
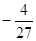 (x
(x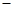 9)
9)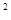 +12
+12 ��x=12ʱ��y =
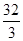
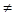
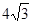 ��
����С����һ�˲��ܰѸ߶������O��ֱ�Ӵ�����A�㣮
��1�������⣬������ϵ�л�����ͼ����֪OA��ˮƽ����OC�ļн�Ϊ30�㣬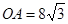 ����ֱ�������ο����A�����ꡣ
����ֱ�������ο����A�����ꡣ
��2�����������֪�������ߵĶ�������Ϊ��9��12��������ԭ�㣨0��0�����趥��ʽ���������ߵĽ���ʽ���ѵ�A�ĺ�����x=12���������߽���ʽ��������ֵ���A���������Ƿ������
 ����ֱ�������ο����A�����ꡣ
����ֱ�������ο����A�����ꡣ��2�����������֪�������ߵĶ�������Ϊ��9��12��������ԭ�㣨0��0�����趥��ʽ���������ߵĽ���ʽ���ѵ�A�ĺ�����x=12���������߽���ʽ��������ֵ���A���������Ƿ������

��ϰ��ϵ�д�
 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д�
�����Ŀ
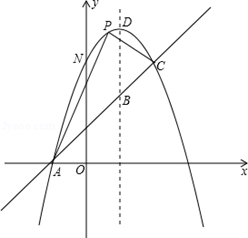
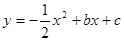 ��ͼ��A��2��0��B��0��-6������
��ͼ��A��2��0��B��0��-6������
 �ύ�ڵ�C������BA��BC�����ABC�����
�ύ�ڵ�C������BA��BC�����ABC����� �Ķ��κ���
�Ķ��κ��� ������˵����ȷ���ǣ� ��
������˵����ȷ���ǣ� �� ��Ľ�������Ϊ��0��2��
��Ľ�������Ϊ��0��2�� ʱ��
ʱ�� ��ͼ��õ�
��ͼ��õ� ��ͼ����������
��ͼ���������� Ԫ�����ӵĿ���
Ԫ�����ӵĿ��� �ף�
�ף� ��y��Ľ��������ǣ�������
��y��Ľ��������ǣ�������