题目内容
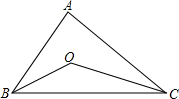
如图,点O是△ABC的内角平分线的交点,O′是△ABC的外角平分线的交点
求证:(1)∠AOB=90°+
∠C;
(2)∠AO′B=90°-
∠C.

求证:(1)∠AOB=90°+
| 1 |
| 2 |
(2)∠AO′B=90°-
| 1 |
| 2 |

证明:(1)如图∵在△ABC中,∠C+∠CAB+∠ABC=180°,
在△AOB中,∠AOB+∠OAB+∠OBA=180°,
∵AO,BO分别是∠CAB和∠ABC的平分线,
∴∠CAB=2∠OAB,∠ABC=2∠OBA,
∴∠ABO+
∠CAB+
∠ABC=180°,
又∵在△ABC中,∠C+∠CAB+∠ABC=180°
∴∠AOB=
∠C+90°;
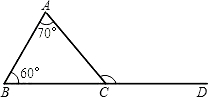
证明:(2)O′是△ABC的外角平分线的交点,
则∠O′AB=
∠EAB=
(180°-∠CAB)=90°-
∠CAB,
∠ABO′=
∠ABF=90°-
∠CBA,
∴∠O′AB+∠ABO′=180°-
(∠CAB+∠CBA)
又∵∠CAB+∠CBA=180°-∠C,
∴∠O′AB+∠ABO′=90°+
∠C,
在△ABO′中利用内角和定理得到:
∠AO′B=180°-(∠O′AB+∠O′BA)=180°-(90°+
∠C)=90°-
∠C.
在△AOB中,∠AOB+∠OAB+∠OBA=180°,
∵AO,BO分别是∠CAB和∠ABC的平分线,
∴∠CAB=2∠OAB,∠ABC=2∠OBA,
∴∠ABO+
| 1 |
| 2 |
| 1 |
| 2 |
又∵在△ABC中,∠C+∠CAB+∠ABC=180°
∴∠AOB=
| 1 |
| 2 |
证明:(2)O′是△ABC的外角平分线的交点,
则∠O′AB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∠ABO′=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠O′AB+∠ABO′=180°-
| 1 |
| 2 |
又∵∠CAB+∠CBA=180°-∠C,
∴∠O′AB+∠ABO′=90°+
| 1 |
| 2 |
在△ABO′中利用内角和定理得到:
∠AO′B=180°-(∠O′AB+∠O′BA)=180°-(90°+
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目