题目内容
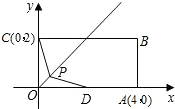
如图,在矩形OABC中,已知A,C两点的坐标分别为A(4,0),C(0,2),D为OA的中点.设点P是∠AOC平分线 上的一个动点(不与点O重合).
上的一个动点(不与点O重合).
(1)试证明:无论点P运动到何处,PC总与PD相等;
(2)当点P运动到与点B的距离最小时,求P的坐标;
(3)已知E(1,-1),当点P运动到何处时,△PDE的周长最小?求出此时点P的坐标和△PDE的周长.
 上的一个动点(不与点O重合).
上的一个动点(不与点O重合).(1)试证明:无论点P运动到何处,PC总与PD相等;
(2)当点P运动到与点B的距离最小时,求P的坐标;
(3)已知E(1,-1),当点P运动到何处时,△PDE的周长最小?求出此时点P的坐标和△PDE的周长.
分析:(1)由A(4,0),C(0,2),D为OA的中点,得到D点坐标为(2,0),则OC=OD,而点P是∠AOC平分线上的一个动点(不与点O重合),根据角平分线的性质有
∠COP=∠DOP=45°,再根据三角形全等的判定方法易得△POC≌△POD,则PC=PD;
(2)过B作BP垂直∠AOC的平分线于P点,过P点作PN⊥x轴于N,交BC于M点,OP交BC于H点,易得△PHM、△COH和△PON都是等腰直角三角形,△PHB是也等腰直角三角形,得到PM垂直平分BH,而CH=CO=2,则BH=2,得到PM=
BH=1,于是有ON=PN=1+2=3,根据坐标的表示方法即可得到P点坐标;
(3)连CE交∠AOC的平分线于P点,连PD、CD,ED,由OC=OD,OP平分直角AOC得到OP垂直平分CD,则PC=PD,得到PD+PE=PC+PE=CE,根据两点之间线段确定此时△PDE的周长最小,然后利用待定系数法求出直线CE的解析式为y=-3x+2,根据P点的横纵坐标相等即可得到P点坐标为(
,
),再利用勾股定理分别计算出CE=
=
,DE=
=
,即可得到此时△PDE的周长.
∠COP=∠DOP=45°,再根据三角形全等的判定方法易得△POC≌△POD,则PC=PD;
(2)过B作BP垂直∠AOC的平分线于P点,过P点作PN⊥x轴于N,交BC于M点,OP交BC于H点,易得△PHM、△COH和△PON都是等腰直角三角形,△PHB是也等腰直角三角形,得到PM垂直平分BH,而CH=CO=2,则BH=2,得到PM=
| 1 |
| 2 |
(3)连CE交∠AOC的平分线于P点,连PD、CD,ED,由OC=OD,OP平分直角AOC得到OP垂直平分CD,则PC=PD,得到PD+PE=PC+PE=CE,根据两点之间线段确定此时△PDE的周长最小,然后利用待定系数法求出直线CE的解析式为y=-3x+2,根据P点的横纵坐标相等即可得到P点坐标为(
| 1 |
| 2 |
| 1 |
| 2 |
| 32+12 |
| 10 |
| 12+12 |
| 2 |
解答:(1)证明:∵A(4,0),C(0,2),D为OA的中点,
∴D点坐标为(2,0),
∴OC=OD,
又∵点P是∠AOC平分线上的一个动点(不与点O重合),
∴∠COP=∠DOP=45°,
∴△POC≌△POD,
∴PC=PD,
即无论点P运动到何处,PC总与PD相等;
(2)解:过B作BP垂直∠AOC的平分线于P点,过P点作PN⊥x轴于N,交BC于M点,OP交BC于H点,如图,
∵OP平分∠AOC,
∴∠COP=∠NOP=45°,
∴△PHM、△COH和△PON都是等腰直角三角形,
∴△PHB是等腰直角三角形,
∴PM垂直平分BH,
∴CH=CO=2,
∴BH=4-2=2,
∴PM=
BH=1,
∴ON=PN=1+2=3,
∴P点坐标为(3,3);
(3 )解:连CE交∠AOC的平分线于P点,连PD、CD,ED,如图,
)解:连CE交∠AOC的平分线于P点,连PD、CD,ED,如图,
∵OC=OD,OP平分直角AOC,
∴OP垂直平分CD,
∴PC=PD,
∴PD+PE=PC+PE=CE,
此时△PDE的周长最小,
设直线CE的解析式为y=kx+b(k≠0),
把C(0,2)、E(1,-1)分别代入得,b=2,k+b=-1,解得k=-3,b=2,
∴直线CE的解析式为y=-3x+2,
而P点的横纵坐标相等,设P(a,a),把P点坐标代入y=-3x+2得,a=-3a+2,解得a=
,
∴P点坐标为(
,
),
∵CE=
=
,DE=
=
,
∴此时△PDE的周长=
+
.
∴D点坐标为(2,0),
∴OC=OD,
又∵点P是∠AOC平分线上的一个动点(不与点O重合),
∴∠COP=∠DOP=45°,
∴△POC≌△POD,
∴PC=PD,
即无论点P运动到何处,PC总与PD相等;
(2)解:过B作BP垂直∠AOC的平分线于P点,过P点作PN⊥x轴于N,交BC于M点,OP交BC于H点,如图,

∵OP平分∠AOC,
∴∠COP=∠NOP=45°,
∴△PHM、△COH和△PON都是等腰直角三角形,
∴△PHB是等腰直角三角形,
∴PM垂直平分BH,
∴CH=CO=2,
∴BH=4-2=2,
∴PM=
| 1 |
| 2 |
∴ON=PN=1+2=3,
∴P点坐标为(3,3);
(3
 )解:连CE交∠AOC的平分线于P点,连PD、CD,ED,如图,
)解:连CE交∠AOC的平分线于P点,连PD、CD,ED,如图,∵OC=OD,OP平分直角AOC,
∴OP垂直平分CD,
∴PC=PD,
∴PD+PE=PC+PE=CE,
此时△PDE的周长最小,
设直线CE的解析式为y=kx+b(k≠0),
把C(0,2)、E(1,-1)分别代入得,b=2,k+b=-1,解得k=-3,b=2,
∴直线CE的解析式为y=-3x+2,
而P点的横纵坐标相等,设P(a,a),把P点坐标代入y=-3x+2得,a=-3a+2,解得a=
| 1 |
| 2 |
∴P点坐标为(
| 1 |
| 2 |
| 1 |
| 2 |
∵CE=
| 32+12 |
| 10 |
| 12+12 |
| 2 |
∴此时△PDE的周长=
| 2 |
| 10 |
点评:本题考查了轴对称-最短路线问题:通过对称,把两条线段的和转化为一条线段,利用两点之间线段最短解决问题.也考查了垂线段最短、勾股定理、矩形的性质和坐标变换以及待定系数法求一次函数的解析式.

练习册系列答案
相关题目
 出此时点P的坐标和△PDE的周长.
出此时点P的坐标和△PDE的周长.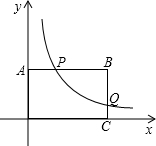 AB的中点,设点P的横坐标为a.
AB的中点,设点P的横坐标为a. (2012•莆田质检)如图,在矩形OABC中,OA、OC两边分别在x轴、y轴的正半轴上,OA=3,OC=2,过OA边上的D点,沿着BD翻折△ABD,点A恰好落在BC边上的点E处,反比例函数
(2012•莆田质检)如图,在矩形OABC中,OA、OC两边分别在x轴、y轴的正半轴上,OA=3,OC=2,过OA边上的D点,沿着BD翻折△ABD,点A恰好落在BC边上的点E处,反比例函数