��Ŀ����
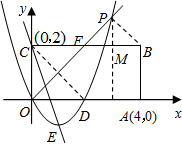
��ͼ���ھ���OABC�У���֪A��C���������ֱ�ΪA��4��0����C��0��2����DΪOA���е㣮���P�ǡ�AOC ƽ�����ϵ�һ�����㣨�����O�غϣ���
ƽ�����ϵ�һ�����㣨�����O�غϣ�����1����֤�������۵�P�˶����δ���PC����PD��ȣ�
��2������P�˶������B�ľ�����Сʱ����ȷ����O��P��D����������ߵĽ���ʽ��
��3�����E�ǣ�2������ȷ�������ߵĶ��㣬����P�˶����δ�ʱ����PDE���ܳ���С�������ʱ��P������͡�PDE���ܳ���
��4�����N�Ǿ���OABC�ĶԳ����ģ��Ƿ���ڵ�P��ʹ��CPN=90�㣿�����ڣ���ֱ��д����P�����꣮
�����������ۺϿ�����������ȫ�ȡ�һ�κ��������κ��������߶���̺�̽���Ե����⣮
��1��ͨ����POC�ա�POD��֤��PC=PD��
��2������Ҫȷ��P���λ�ã������P��F�������꣬���ô���ϵ������������߽���ʽ��
��3�������������öԳ���ȷ����P��λ����EC���AOC��ƽ���ߵĽ��㣬��������������ֱ��CE�Ľ���ʽ�������P�����꣮������ġ�PED���ܳ���
��4��Ҫʹ��CPN=90�㣬��P������CN���е�ΪԲ����CNΪֱ����Բ���ƽ���ߵĽ��㣬�ɴ˾�����д��P������꣮
��1��ͨ����POC�ա�POD��֤��PC=PD��
��2������Ҫȷ��P���λ�ã������P��F�������꣬���ô���ϵ������������߽���ʽ��
��3�������������öԳ���ȷ����P��λ����EC���AOC��ƽ���ߵĽ��㣬��������������ֱ��CE�Ľ���ʽ�������P�����꣮������ġ�PED���ܳ���
��4��Ҫʹ��CPN=90�㣬��P������CN���е�ΪԲ����CNΪֱ����Բ���ƽ���ߵĽ��㣬�ɴ˾�����д��P������꣮
��� �⣺��1���ߵ�D��OA���е㣬
�⣺��1���ߵ�D��OA���е㣬
��OD=2��
��OD=OC��
�֡�OP�ǡ�COD�Ľ�ƽ���ߣ�
���POC=��POD=45�㣬
���POC�ա�POD��
��PC=PD��
��2������B����AOC��ƽ���ߵĴ��ߣ�����ΪP����P��Ϊ����
��֪��F������Ϊ��2��2������BF=2����PM��BF��
�ߡ�PBF�ǵ���ֱ�������Σ�
��PM=
BF=1��
���P��������3��3����
�������߾���ԭ�㣬
���������ߵĽ���ʽΪy=ax2+bx��
�֡������߾�����P��3��3���͵�D��2��0����
����
���
�������ߵĽ���ʽΪy=x2-2x��
��3���ɵ���ֱ�������εĶԳ���֪D����ڡ�AOC��ƽ���ߵĶԳƵ㼴ΪC�㣮
����EC�������AOC��ƽ���ߵĽ��㼴Ϊ�����P�㣨��ΪPE+PD=EC��������֮���߶���̣�����ʱ��PED���ܳ���С��
��������y=x2-2x�Ķ���E�����꣨1��-1����C������꣨0��2����
��CE����ֱ�ߵĽ���ʽΪy=kx+b��
����
��
���
��
��CE����ֱ�ߵĽ���ʽΪy=-3x+2��
��P����
��
���
��
�ʵ�P������Ϊ(
��
)��
��PED���ܳ�����CE+DE=
+
��
��4��������ڷ���������P�㣮���εĶԳ�����Ϊ�Խ��ߵĽ��㣬��N��2��1����
�ٵ�P����N���Ϸ�ʱ���ɣ�2��֪F��2��2�����ҡ�NFC=90�㣬��ȻF�����P���Ҫ��P��2��2����
�ڵ�P����N���·�ʱ����P��a��a������C��0��2����N��2��1�������ɹ��ɶ����ã�CP2+PN2=CN2����a2+��a-2��2+��2-a��2+��1-a��2=5����4a2-10a+4=0�����a=
��a=2����P��
��
����
���Ͽ�֪�����ڵ�P��ʹ��CPN=90�ȣ���������(
��
)��2��2����
 �⣺��1���ߵ�D��OA���е㣬
�⣺��1���ߵ�D��OA���е㣬��OD=2��
��OD=OC��
�֡�OP�ǡ�COD�Ľ�ƽ���ߣ�
���POC=��POD=45�㣬
���POC�ա�POD��
��PC=PD��
��2������B����AOC��ƽ���ߵĴ��ߣ�����ΪP����P��Ϊ����
��֪��F������Ϊ��2��2������BF=2����PM��BF��
�ߡ�PBF�ǵ���ֱ�������Σ�
��PM=
| 1 |
| 2 |
���P��������3��3����
�������߾���ԭ�㣬
���������ߵĽ���ʽΪy=ax2+bx��
�֡������߾�����P��3��3���͵�D��2��0����
����
|
���
|
�������ߵĽ���ʽΪy=x2-2x��
��3���ɵ���ֱ�������εĶԳ���֪D����ڡ�AOC��ƽ���ߵĶԳƵ㼴ΪC�㣮
����EC�������AOC��ƽ���ߵĽ��㼴Ϊ�����P�㣨��ΪPE+PD=EC��������֮���߶���̣�����ʱ��PED���ܳ���С��
��������y=x2-2x�Ķ���E�����꣨1��-1����C������꣨0��2����
��CE����ֱ�ߵĽ���ʽΪy=kx+b��
����
|
���
|
��CE����ֱ�ߵĽ���ʽΪy=-3x+2��
��P����
|
���
|
�ʵ�P������Ϊ(
| 1 |
| 2 |
| 1 |
| 2 |
��PED���ܳ�����CE+DE=
| 10 |
| 2 |
��4��������ڷ���������P�㣮���εĶԳ�����Ϊ�Խ��ߵĽ��㣬��N��2��1����
�ٵ�P����N���Ϸ�ʱ���ɣ�2��֪F��2��2�����ҡ�NFC=90�㣬��ȻF�����P���Ҫ��P��2��2����
�ڵ�P����N���·�ʱ����P��a��a������C��0��2����N��2��1�������ɹ��ɶ����ã�CP2+PN2=CN2����a2+��a-2��2+��2-a��2+��1-a��2=5����4a2-10a+4=0�����a=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
���Ͽ�֪�����ڵ�P��ʹ��CPN=90�ȣ���������(
| 1 |
| 2 |
| 1 |
| 2 |
�������������ı��λ������ε��ۺϿ��飬�ǽ������п���һ���ȵ����⣮�����������⣬ͨ����Ҫѧ����Ϥ���ն�����뺯���ĸ��������ʼ�����֮�����ϵ��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ����ʱ��P������͡�PDE���ܳ���
����ʱ��P������͡�PDE���ܳ���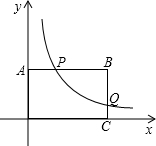 AB���е㣬���P�ĺ�����Ϊa��
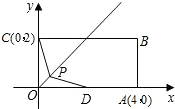
AB���е㣬���P�ĺ�����Ϊa�� ��2012•�����ʼ죩��ͼ���ھ���OABC�У�OA��OC���߷ֱ���x�ᡢy����������ϣ�OA=3��OC=2����OA���ϵ�D�㣬����BD���ۡ�ABD����Aǡ������BC���ϵĵ�E��������������
��2012•�����ʼ죩��ͼ���ھ���OABC�У�OA��OC���߷ֱ���x�ᡢy����������ϣ�OA=3��OC=2����OA���ϵ�D�㣬����BD���ۡ�ABD����Aǡ������BC���ϵĵ�E��������������