ƒøƒ⁄»ð
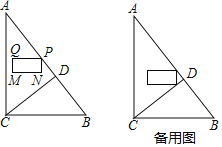
°æƒø°ø»ÁÕº1£¨‘⁄»ÒΩ«°˜ABC÷–£¨AB=5£¨tanC=3£¨BD°ÕAC”⁄µ„D£¨BD=3£¨µ„P¥”µ„A≥ˆ∑¢£¨“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»—ÿABœÚ÷’µ„B‘À∂Ø£¨π˝µ„P◊˜PE°ŒACΩª±þBC”⁄µ„E£¨“‘PEŒ™±þ◊˜Rt°˜PEF£¨ π°œEPF=90°„£¨µ„F‘⁄µ„Pµƒœ¬∑Ω£¨«“EF°ŒAB£Æ…Ë°˜PEF”ΰ˜ABD÷ÿµ˛≤ø∑÷Õº–Œµƒ√ʪ˝Œ™S£®∆Ω∑Ωµ•Œª£©£®S£æ0£©£¨µ„Pµƒ‘À∂Ø ±º‰Œ™t£®√Σ©
£®t£æ0£©£Æ
£®1£©«Ûœþ∂ŒACµƒ≥§£Æ
£®2£©µ±°˜PEF”ΰ˜ABD÷ÿµ˛≤ø∑÷Õº–ŒŒ™Àƒ±þ–Œ ±£¨«ÛS”Ît÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£¨≤¢–¥≥ˆtµƒ»°÷µ∑∂Œß£Æ
£®3£©»Ù±þEFÀ˘‘⁄÷±œþ”αþACΩª”⁄µ„Q£¨¡¨Ω·PQ£¨»ÁÕº2£¨÷±Ω”–¥≥ˆ°˜ABCµƒƒ≥“ª∂•µ„µΩP°¢Q¡Ωµ„æý¿Îœýµ» ±tµƒ÷µ£Æ
°æ¥∞∏°ø£®1£©5£®2£©S=![]() £®5©Åt£©2£®3£©◊€…œÀ˘ ˆ£¨t=
£®5©Åt£©2£®3£©◊€…œÀ˘ ˆ£¨t=![]() sªÚ
sªÚ![]() sªÚ
sªÚ![]() s ±£¨¬˙◊„ƒø“™«Û
s ±£¨¬˙◊„ƒø“™«Û
°æΩ‚Œˆ°ø∑÷Œˆ: £®1£©‘⁄Rt°˜ABD÷–£¨¿˚”√π¥π…∂®¿Ì«Û≥ˆAD£¨‘⁄Rt°˜BDC÷–£¨«Û≥ˆCDº¥ø…£Æ
£®2£©∑÷2÷÷«È–Œ«ÛΩ‚£∫»ÁÕº1÷–£¨µ±0£ºt°Ð1 ±£¨÷ÿµ˛≤ø∑÷ «Àƒ±þ–ŒPMDN£Æ»ÁÕº2÷–£¨µ±![]() °Ðt£º5 ±£¨÷ÿµ˛≤ø∑÷ «Àƒ±þ–ŒPNMF£Æ
°Ðt£º5 ±£¨÷ÿµ˛≤ø∑÷ «Àƒ±þ–ŒPNMF£Æ
£®3£©»ÁÕº5÷–£¨µ±PQµƒ¥π÷±∆Ω∑÷œþæ≠π˝µ±A ±£Æ∏˘æðPE=PA£¨ø…µ√t=5-tΩ‚æˆŒ £ƻÁÕº6÷–£¨µ±PQµƒ¥π÷±∆Ω∑÷œþæ≠π˝µ„B ±£¨◊˜EN°ÕAC”⁄N£¨EPΩªBD”⁄M£Æ‘⁄Rt°˜BQD÷–£¨∏˘æðBQ2=QD2+BD2£¨¡–≥ˆ∑Ω≥ú¥ø…Ω‚æˆŒ Â.
œÍΩ‚:
£®1£©‘⁄Rt°˜ABD÷–£¨°œBDA=90°„£¨AB=5£¨BD=3£¨
°ýAD=![]() =
=![]() =4£¨
=4£¨
‘⁄Rt°˜BCD÷–£¨°œBDC=90°„£¨BD=3£¨tanc=3£¨°ýCD=![]() =
=![]() =1£¨
=1£¨
°ýAC=AD+CD=4+1=5£Æ
£®2£©»ÁÕº1÷–£¨µ±0£ºt°Ð1 ±£¨÷ÿµ˛≤ø∑÷ «Àƒ±þ–ŒPMDN£Æ
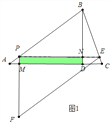


“◊÷™PA=t£¨AM=![]() t£¨PM=
t£¨PM=![]() t£¨DM=4©Å
t£¨DM=4©Å![]() t£¨
t£¨
°ýS=![]() t£®4©Å
t£®4©Å![]() t£©=©Å
t£©=©Å![]() t2+
t2+![]() t£Æ
t£Æ
»ÁÕº2÷–£¨µ±![]() °Ðt£º5 ±£¨÷ÿµ˛≤ø∑÷ «Àƒ±þ–ŒPNMF£Æ
°Ðt£º5 ±£¨÷ÿµ˛≤ø∑÷ «Àƒ±þ–ŒPNMF£Æ
°þAB=5£¨AC=AD+CD=4+1=5£¨
°ýAC=AB£¨
“◊÷§PB=PE=5©Åt£¨PF=![]() £®5©Åt£©£¨PN=
£®5©Åt£©£¨PN=![]() £®5©Åt£©£¨
£®5©Åt£©£¨
S=![]() £®5©Åt£©
£®5©Åt£©![]() £®5©Åt£©©Å
£®5©Åt£©©Å![]()
![]() £®5©Åt£©
£®5©Åt£©![]()
![]() £®5©Åt£©=
£®5©Åt£©=![]() £®5©Åt£©2£Æ
£®5©Åt£©2£Æ
£®3£©»ÁÕº3÷–£¨µ±AµΩP°¢Qæý¿Îœýµ» ±£Æ
“◊÷™Àƒ±þ–ŒAPEQ ±¡‚–Œ£¨°ýPE=PA£¨º¥t=5©Åt£¨°ýt=![]() £Æ
£Æ
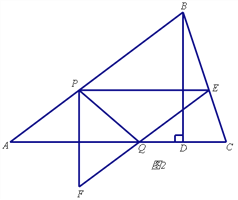
»ÁÕº4÷–£¨µ±BµΩP°¢Qæý¿Îœýµ» ±£¨◊˜EN°ÕAC”⁄N£¨EPΩªBD”⁄M£Æ


“◊÷™Àƒ±þ–ŒPENG «æÿ–Œ£¨Àƒ±þ–ŒDMEN «æÿ–Œ£¨°ýPG=EN=![]() t£¨EM=DN=PE©ÅPM=
t£¨EM=DN=PE©ÅPM=![]() £®5©Åt£©£¨
£®5©Åt£©£¨
QN=![]() EN=
EN=![]() t£¨°ýQD=4©Å£®5©Åt£©=t©Å1£¨‘⁄Rt°˜BQD÷–£¨°þBQ2=QD2+BD2£¨
t£¨°ýQD=4©Å£®5©Åt£©=t©Å1£¨‘⁄Rt°˜BQD÷–£¨°þBQ2=QD2+BD2£¨
°ý£®5©Åt£©2=32+£®t©Å1£©2£¨°ýt=![]() £Æ
£Æ
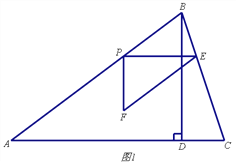
»ÁÕº5÷–£¨µ±CµΩP°¢Qæý¿Îœýµ» ±£¨◊˜PM°ÕAC”ÎM£¨¡¨Ω”PC£Æ
”…PC=CQ£¨ø…µ√£∫£®![]() t£©2+£®5©Å
t£©2+£®5©Å![]() t£©2=t2£¨Ω‚µ√t=
t£©2=t2£¨Ω‚µ√t=![]()
◊€…œÀ˘ ˆ£¨t=![]() sªÚ
sªÚ![]() sªÚ
sªÚ![]() s ±£¨¬˙◊„ƒø“™«Û£Æ
s ±£¨¬˙◊„ƒø“™«Û£Æ
µ„æ¶: ±æÂøº≤È»˝Ω«–Œ◊€∫œÃ‚°¢Ω‚÷±Ω«»˝Ω«–Œ°¢π¥π…∂®¿Ì°¢»ÒΩ«»˝Ω«∫Ø ˝µ»÷™ ∂£¨Ω‚µƒπÿº¸ «¡ÈªÓ‘À”√À˘—ß÷™ ∂Ω‚æˆŒ £¨—ߪ·”√∑÷¿ýÃ÷¬€µƒÀºœÎÀºøºŒ £¨—ߪ·ππΩ®∑Ω≥ÃΩ‚æˆŒ £¨ Ù”⁄÷–øº—π÷·Ã‚.