题目内容
【题目】如图,已知A(4,2)、B(a,4)是一次函数y=kx+b的图象与反比例函数![]() 的图象的两个交点;
的图象的两个交点;
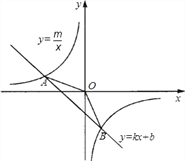
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
【答案】(1)反比例函数的解析式为![]() ,一次函数的解析式为y=-x-2(2)-4<x<0或x>2
,一次函数的解析式为y=-x-2(2)-4<x<0或x>2
【解析】试题分析:(1)把A点坐标代入反比例函数解析式求出m的值,再把B点坐标代入反比例函数解析式求出a的值,从而得出点B的坐标,根据点A、B的坐标利用待定系数法即可求出直线AB的解析式;
(2)由两函数图象的上下位置关系结合交点的横坐标,即可得出使一次函数值小于反比例函数值的x的取值范围.
试题解析:
解:(1)∵m=xy=(-4)×2=-8,
∴反比例函数的解析式为y=![]() .
.
∴-4a=-8,
∴a=2,
y=kx+b过A(-4,2),B(2,-4)两点,
∴![]() ,
,
解得![]() .
.
故一次函数的解析式为y=-x-2;
(2)观察函数图象可知:当-4<x<0或x>2时,一次函数图象在反比例函数图象下方,
∴一次函数的值小于反比例函数值的x的取值范围:-4<x<0或x>2.

练习册系列答案
相关题目
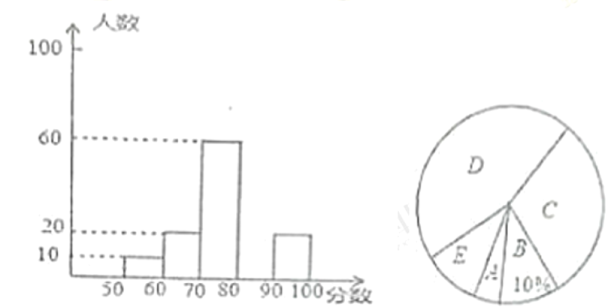
【题目】七年级数学研究学习小组在某↑字路口随机调查部分市民对“社会主义核心价值观”的了解情况,统计结果后绘制了如图的两副不完整的统计图,请结合图中相关数据回答下列问题:
得分 | |
|
|
|
|
|
|
|
|
|
|
(1)本次调查的总人数为 人, 在扇形统计图中“心所在扇形的圆心角的度数为 :
(2)补全频数分布图:
(3)若在这周里,该路口共有![]() 人通过,请估计得分超过
人通过,请估计得分超过![]() 的约有多少人?
的约有多少人?