题目内容
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
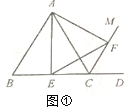
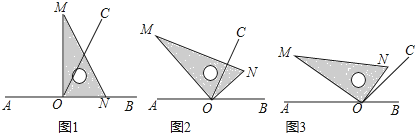
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
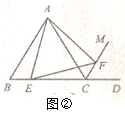
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
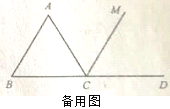
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=![]() ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.
【答案】(1)25°;(2)25°;(3)70°.
【解析】
试题分析:(1)根据∠MON和∠BOC的度数可以得到∠MON的度数.
(2)根据OC是∠MOB的角平分线,∠BOC=65°可以求得∠BOM的度数,由∠NOM=90°,可得∠BON的度数,从而可得∠CON的度数.
(3)由∠BOC=65°,∠NOM=90°,∠NOC=![]() ∠AOM,从而可得∠NOC的度数,由∠BOC=65°,从而得到∠NOB的度数.
∠AOM,从而可得∠NOC的度数,由∠BOC=65°,从而得到∠NOB的度数.
解:(1)∵∠MON=90°,∠BOC=65°,
∴∠MOC=∠MON﹣∠BOC=90°﹣65°=25°.
故答案为:25°.
(2)∵∠BOC=65°,OC是∠MOB的角平分线,
∴∠MOB=2∠BOC=130°.
∴∠BON=∠MOB﹣∠MON
=130°﹣90°
=40°.
∠CON=∠COB﹣∠BON
=65°﹣40°
=25°.
(3)∵∠NOC![]() ∠AOM,
∠AOM,
∴∠AOM=4∠NOC.
∵∠BOC=65°,
∴∠AOC=∠AOB﹣∠BOC
=180°﹣65°
=115°.
∵∠MON=90°,
∴∠AOM+∠NOC=∠AOC﹣∠MON
=115°﹣90°
=25°.
∴4∠NOC+∠NOC=25°.
∴∠NOC=5°.
∴∠NOB=∠NOC+∠BOC=70°.

【题目】为鼓励民众节约用电,城镇居民生活用电电费目前实行梯度收费,具体标准如下表:
月用电量(单位:千瓦时) | 单价(单位:元) |
150以内(含150) | 0.5 |
超过150但不超过300的部分(含300) | 0.6 |
300以上(不含300)的部分 | 0.8 |
(1)若月用电100千瓦时,应交电费多少元?若月用电200千瓦时,应交电费多少元?
(2)若某用户12月应交电费93元,该用户12月的用电量是多少?