题目内容
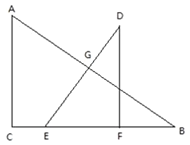
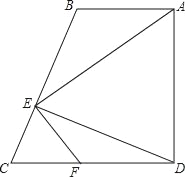
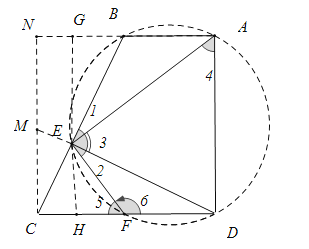
【题目】如图,在四边形ABCD中,AB∥CD,∠ADC=90°,DE⊥BC于E,连AE,FE⊥AE交CD于点F.
(1)求证:△AED∽△FEC;
(2)若AB=2![]() ,求DF的值;
,求DF的值;
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)根据条件可以得出∠EFC=∠EAD,∠CEF=∠AED,进而可以证明△AED∽△FEC.
(2)根据条件可以证明A、D、F、B、A四点共圆,由∠BEA=∠FED,推出结论.
(3)设AB=a,CD=b,通过辅助线,利用方程的思想,解决问题.
试题解析:解:(1)∵DE⊥BC,EF⊥AE,∴∠BED=∠CED=90°.∵∠2+∠3=90°,∠2+∠CEF=90°,∴∠CEF=∠3.∵∠AEF=∠ADF=90°,∴∠6+∠4=180°.∵∠5+∠6=180°,∴∠5=∠4,∴△ADE∽△FEC.
(2)∵∠1+∠3=90°,∠2+∠3=90°,∴∠1=∠2.∵AB∥CD,∠ADC=90°,∴∠BAD+∠ADC=180°,∴∠BAD=90°.∵∠BED+∠BAD=180°,∴四边形ABCD四点共圆.∵∠AEF+∠ADF=180°,∴四边形AEFD四点共圆,∴A、B、E、F、D五点共圆.∵∠1=∠2,∴DF=AB=2![]() .
.
(3)作CN⊥AB交AB的延长线于N,过点E作EG⊥AN垂足为G交CD于H,延长DE交CN于M.∵![]() =
=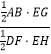 =2,AB=FD,∴EG=2EH.∵GB∥CH,∴△EGB∽△EHC,∴
=2,AB=FD,∴EG=2EH.∵GB∥CH,∴△EGB∽△EHC,∴![]() =
=![]() =2,设EC=a,AB=x,CD=y,则EB=2a.∵∠NCD=∠ADC=∠DAN=90°,∴四边形ADCN是矩形.∵AD=DC,∴四边形ADCN是正方形,∴AN=CN=CD=y,NB=y﹣x.∵∠NCB+∠CMD=90°,∠CMD+∠MDC=90°,∴∠NCB=∠MDC.∵CN=CD,∴△CNB≌△DCM,∴CM=BN=y﹣x,DM=BC=3a.∵∠MCD=∠MEC,∠CME=∠CMD,∴△MCE∽△MDC,∴
=2,设EC=a,AB=x,CD=y,则EB=2a.∵∠NCD=∠ADC=∠DAN=90°,∴四边形ADCN是矩形.∵AD=DC,∴四边形ADCN是正方形,∴AN=CN=CD=y,NB=y﹣x.∵∠NCB+∠CMD=90°,∠CMD+∠MDC=90°,∴∠NCB=∠MDC.∵CN=CD,∴△CNB≌△DCM,∴CM=BN=y﹣x,DM=BC=3a.∵∠MCD=∠MEC,∠CME=∠CMD,∴△MCE∽△MDC,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴y2﹣xy=3a2①
,∴y2﹣xy=3a2①
∵CM2+CD2=MD2,∴(y﹣x)2+y2=9a2②
由①②消去a得x2+xy﹣y2=0
∴x=![]() y,(或x=
y,(或x=![]() y舍弃)
y舍弃)
∴![]() =
=![]() ,∴
,∴![]() =
=![]() .
.
故答案为:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
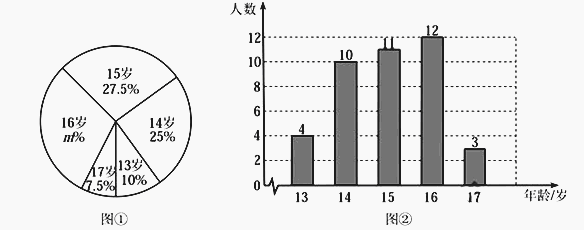
小学生10分钟应用题系列答案【题目】某校为了解全校学生上学期参加“生涯规划”社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
参加社区活动次数的频数、频率
活动次数x | 频数 | 频率 |
0<x≤3 | 10 | 0.20 |
3<x≤6 | a | 0.24 |
6<x≤9 | 16 | 0.32 |
9<x≤12 | 6 | 0.12 |
12<x≤15 | b | m |
15<x≤18 | 2 | n |
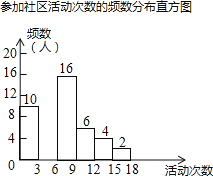
根据以上图表信息,解答下列问题:
(1)表中a= , b= , m= , n= .
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
【题目】为了传承中华优秀传统文化,某校组织八年级学生参加了“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,绘制如下不完整的条形统计图.
汉字听写大赛成绩分数段统计表
分数段 | 频数 |
| 2 |
| 6 |
| 9 |
| 18 |
| 15 |
汉字听写大赛成绩分数段条形统计图

(1)补全条形统计图.
(2)这次抽取的学生成绩的中位数在________的分数段中;这次抽取的学生成绩在![]() 的分数段的人数占抽取人数的百分比是_______.
的分数段的人数占抽取人数的百分比是_______.
(3)若该校八年级一共有学生350名,成绩在90分以上(含90分)为“优”,则八年级参加这次比赛的学生中成绩“优”等的约有多少人?