题目内容
【题目】参照学习反比例函数的过程与方法,探究函数 y1=![]() (x≠0)的图象与性质,因为 y1=
(x≠0)的图象与性质,因为 y1=![]() =1﹣
=1﹣![]() ,即 y1=﹣
,即 y1=﹣![]() +1,所以我们对比函数 y=﹣
+1,所以我们对比函数 y=﹣![]() 来探究画出函数 y1=
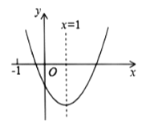
来探究画出函数 y1=![]() (x≠0) 的图象,经历分析解析式、列表、描点、连线过程得到两个函数的图像如图所示.
(x≠0) 的图象,经历分析解析式、列表、描点、连线过程得到两个函数的图像如图所示.
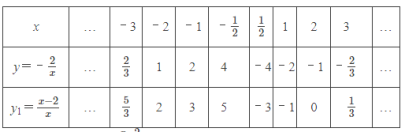
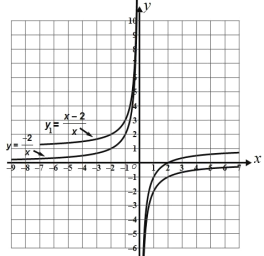
(1)观察:由 y1=![]() 图象可知:
图象可知:
①当 x>0 时,y 随 x的增大而 (填“增大”或“减小”)
②y1=![]() 的图象可以由 y=﹣
的图象可以由 y=﹣![]() 的图象向 平移 个单位长度得到.
的图象向 平移 个单位长度得到.
③y1 的取值范围是 .
(2)探究:①若直线 l 对应的函数关系式为 y2=kx+b,且经过点(﹣1,3)和点(1,﹣1),请再给出的平面直角坐标系中画出 y2,若 y1>y2,则 x 的取值范围为 .
②A(m1,n1),B(m2,n2)在函数 y=![]() 图象上,且 n1+n2=2,求 m1+m2 的值.
图象上,且 n1+n2=2,求 m1+m2 的值.
【答案】(1)①增大,②上,1,③y1≠1;(2)①-1<x<0或x>1,②![]() .
.
【解析】
(1)①②③观察图象即可解决问题;
(2)①根据点(﹣1,3)和点(1,﹣1)即可画出y2=kx+b的图象,可判断这两个点也经过y1=![]() 图象,所以根据图象即可判断y1>y2时x 的取值范围.
图象,所以根据图象即可判断y1>y2时x 的取值范围.
②分别将A、B两点代入y=![]() 中,由n1+n2=2可得出关于m1 、m2的等式,对等式进行变形即可得出m1+m2=0.
中,由n1+n2=2可得出关于m1 、m2的等式,对等式进行变形即可得出m1+m2=0.
(1)①当 x>0 时,y 随 x的增大而增大;
②向上平移1个单位得到;
③y1的取值范围为y1≠1;
(2)①因为函数y2=kx+ b经过点(﹣1,3)和点(1,﹣1),
所以其图象如下:
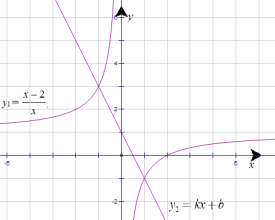
将x=-1代入y1=![]() ,可求得y1=3,所以点(﹣1,3)也在y1=
,可求得y1=3,所以点(﹣1,3)也在y1=![]() 上,
上,
将x=1代入y1=![]() ,可求得y1=-1,所以点(1,-1)也在y1=
,可求得y1=-1,所以点(1,-1)也在y1=![]() 上.
上.
所以根据图象,若y1>y2,则x的取值范围为-1<x<0或x>1.
②∵A(m1,n1),B(m2,n2)在函数 y=![]() 图象上
图象上
∴![]()
∵n1+n2=2
∴![]()
即![]()
即![]() ,
,![]() .
.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案