题目内容
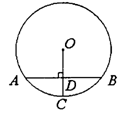
(本题6分)已知:如图,△ABC是等边三角形,D是AB边上的点,将DB绕点D顺时针旋转60°得到线段DE,延长ED交AC于点F,连结DC、AE.
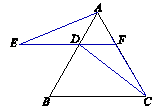
1.(1)求证:△ADE≌△DFC;
2.(2)过点E作EH∥DC交DB于点G,交BC于点H,连结AH.求∠AHE的度数;
3.(3)若BG=![]() ,CH=2,求BC的长.
,CH=2,求BC的长.
1.(1)证明:如图,
∵ 线段DB顺时针旋转60°得线段DE,
∴∠EDB =60°,DE=DB.
∵△ABC是等边三角形,
∴∠B=∠ACB =60°.
∴∠EDB =∠B .
∴EF∥BC.················································ 1分
∴DB=FC,∠ADF=∠AFD =60°.
∴DE=DB=FC,∠ADE=∠DFC =120°,△ADF是等边三角形.
∴AD=DF.
∴ △ADE≌△DFC.
2.(2)由 △ADE≌△DFC,
得AE=DC,∠1=∠2.
∵ED∥BC, EH∥DC,
∴四边形EHCD是平行四边形.
∴EH=DC,∠3=∠4.
∴AE=EH. ······································································································· 3分
∴∠AEH=∠1+∠3=∠2+∠4 =∠ACB=60°.
∴△AEH是等边三角形.
∴∠AHE=60°.
3.(3)设BH=x,则AC= BC =BH+HC= x+2,
由(2)四边形EHCD是平行四边形,
∴ED=HC.
∴DE=DB=HC=FC=2.
∵EH∥DC,
∴△BGH∽△BDC.··························································································· 5分
∴![]() .即
.即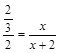 .
.
解得![]() .
.
∴ BC=3.
解析:略

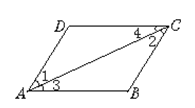
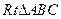 中,
中,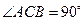 ,以AC为直径作⊙O交AB于点D.
,以AC为直径作⊙O交AB于点D. ,求线段BD的长.
,求线段BD的长.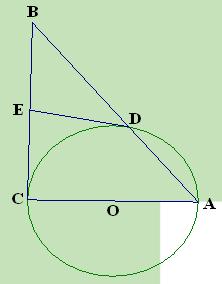
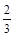 ,CH=2,求BC的长.
,CH=2,求BC的长.