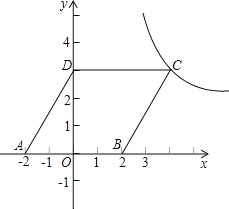题目内容
【题目】(1)阅读理解
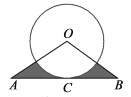
利用旋转变换解决数学问题是一种常用的方法.如图,点![]() 是等边三角形
是等边三角形![]() 内一点,
内一点,![]() ,
,![]() ,
,![]() .求
.求![]() 的度数.
的度数.
为利用已知条件,不妨把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() ,则
,则![]() 的长为_______;在
的长为_______;在![]() 中,易证
中,易证![]() ,且
,且![]() 的度数为________,综上可得
的度数为________,综上可得![]() 的度数为_______;
的度数为_______;
(2)类比迁移
如图,点![]() 是等腰
是等腰![]() 内的一点,
内的一点,![]() ,
,![]() ,
,![]() ,
,![]() .求
.求![]() 的度数;
的度数;
(3)拓展应用
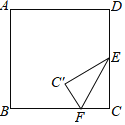
如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长.
的长.
【答案】(1)2, 30°,90°;(2)90°;(3)2![]() .
.
【解析】
(1)由旋转性质、等边三角形的判定可知△CP′P是等边三角形,由等边三角形的性质知∠CP′P=60°,根据勾股定理逆定理可得△AP′P是直角三角形,继而可得答案.
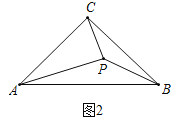
(2)如图2,把△BPC绕点C顺时针旋转90°得△AP'C,连接PP′,同理可得△CP′P是等腰直角三角形和△AP′P是等腰直角三角形,所以∠APC=90°;
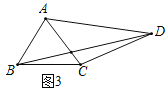
(3)如图3,将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,根据勾股定理求CG的长,就可以得BD的长.
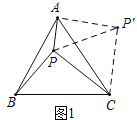
(1)把△BPC绕点C顺时针旋转60°得△AP'C,连接PP′(如图1).
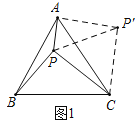
由旋转的性质知△CP′P是等边三角形;
∴P′A=PB=![]() 、∠CP′P=60°、P′P=PC=2,
、∠CP′P=60°、P′P=PC=2,
在△AP′P中,∵AP2+P′A2=12+(![]() )2=4=PP′2;
)2=4=PP′2;
∴△AP′P是直角三角形;
∴∠P′AP=90°.
∵PA=![]() PC,
PC,
∴∠AP′P=30°;
∴∠BPC=∠CP′A=∠CP′P+∠AP′P=60°+30°=90°.
(2)如图2,把△BPC绕点C顺时针旋转90°得△AP'C,连接PP′.
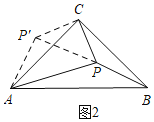
由旋转的性质知△CP′P是等腰直角三角形;
∴P′C=PC=1,∠CPP′=45°、P′P=![]() ,PB=AP'=
,PB=AP'=![]() ,
,
在△AP′P中,∵AP'2+P′P2=(![]() )2+(
)2+(![]() )2=4=AP2;
)2=4=AP2;
∴△AP′P是等腰直角三角形;
∴∠AP′P=90°.
∴∠APP'=45°
∴∠APC=∠APP'+∠CPP'=45°+45°=90°
(3)如图3,
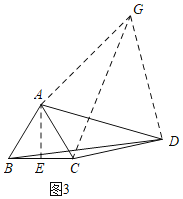
∵AB=AC,
将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,
∵∠BAD=∠CAG,
∴∠BAC=∠DAG,
∵AB=AC,AD=AG,
∴∠ABC=∠ACB=∠ADG=∠AGD,
∴△ABC∽△ADG,
∵AD=2AB,
∴DG=2BC=10,
过A作AE⊥BC于E,
∵∠BAE+∠ABC=90°,∠BAE=∠ADC,
∴∠ADG+∠ADC=90°,
∴∠GDC=90°,
∴CG=![]() ,
,
∴BD=CG=2![]() .
.

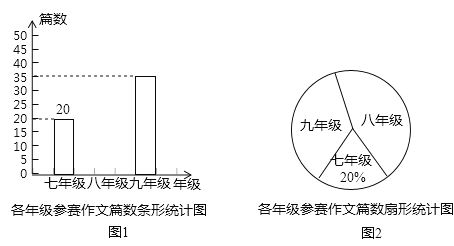
【题目】某学校为了了解九年级学生寒假的阅读情况,随机抽取了该年级的部分学生进行调查,统计了他们每人的阅读本数,设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
阅读本数n(本) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数(名) | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
请根据以上信息回答下列问题:
(1)分别求出统计表中的x,y的值;
(2)求扇形统计图中“优秀”类所在扇形的圆心角的度数;
(3)如果随机去掉一个数据,求众数发生变化的概率,并指出众数变化时,去掉的是哪个数据.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/21/2208296361205760/2209339150721024/STEM/fd85c35161634f71b20809e4321f104b.png]