题目内容
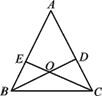
【题目】如图,△ABC中,D,E分别是AC,AB上的点,BD与CE交于点O.给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,哪两个条件可判定△ABC是等腰三角形(用序号写出一种情形):_______.
【答案】①③或②③
【解析】
已知①③条件,先证明△BEO≌△CDO再证明∠ABC=∠ACB最后得到△ABC是等腰三角形;已知②③条件可证明△BEO≌△CDO,再证明△ABC是等腰三角形.
①③或②③.
由①③证明△ABC是等腰三角形.
在△BEO和△CDO中,
∵∠EBO=∠DCO,∠EOB=∠DOC,BE=CD.
∴△BEO≌△CDO,
∴BO=CO,
∴∠OBC=∠OCB,
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
∴AB=AC.
因此△ABC是等腰三角形.
由②③证明△ABC是等腰三角形.
在△BEO和△CDO中,
∵∠BEO=∠CDO,BE=CD,∠EOB=∠DOC,
∴△BEO≌△CDO,
∴BO=CO,
∴∠OBC=∠OCB,
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,AB=AC.
∴△ABC是等腰三角形.
故答案为:①③或②③.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目