题目内容
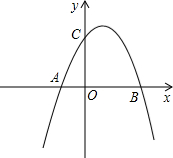如图，抛物线L1：y=-x2-4x+5交x轴于A、B，交y轴于C，顶点为D．
（1）求A、C、B、D四点的坐标及对称轴；
（2）若抛物线L2是抛物线L1沿x轴向左平移3个单位得到的，求抛物线经L2对应的函数表达式．
解：（1）∵当y=0时，-x2+4x+5=0，
即x2-4x-5=0，解得x1=5，x2=-1．
∴A（-1，0）、B（5，0）．
∵当x=0时，y=-02+4×0+5=5，
∴C（0，5）．
∵y=-x2+4x+5=-（x-2）2+9，
∴抛物线L1顶点D的坐标为（2，9），对称轴为x=2；
（2）∵抛物线L2是抛物线L1沿x轴向左平移三个单位得到的，
∴物线L2的解析式是y=-（x-2+3）2+9，
即y=-（x+1）2+9．
分析：（1）抛物线L1中，令x=0，可求出C点坐标；令y=0，可求出A、B的坐标；将原抛物线的解析式化为顶点式，即可求出抛物线的顶点D的坐标及对称轴方程；
（2）根据二次函数图象左加右减的平移规律进行求解．
点评：此题主要考查了二次函数解析式顶点坐标、对称轴、与坐标轴交点坐标的求法，以及二次函数图象的平移等知识，属于基础知识，需牢固掌握．
即x2-4x-5=0，解得x1=5，x2=-1．
∴A（-1，0）、B（5，0）．
∵当x=0时，y=-02+4×0+5=5，
∴C（0，5）．
∵y=-x2+4x+5=-（x-2）2+9，
∴抛物线L1顶点D的坐标为（2，9），对称轴为x=2；
（2）∵抛物线L2是抛物线L1沿x轴向左平移三个单位得到的，
∴物线L2的解析式是y=-（x-2+3）2+9，
即y=-（x+1）2+9．
分析：（1）抛物线L1中，令x=0，可求出C点坐标；令y=0，可求出A、B的坐标；将原抛物线的解析式化为顶点式，即可求出抛物线的顶点D的坐标及对称轴方程；
（2）根据二次函数图象左加右减的平移规律进行求解．
点评：此题主要考查了二次函数解析式顶点坐标、对称轴、与坐标轴交点坐标的求法，以及二次函数图象的平移等知识，属于基础知识，需牢固掌握．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
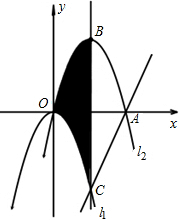如图，抛物线l1：y=-x2平移得到抛物线l2，且经过点O（0，0）和点A（4，0），l2的顶点为点B，它的对称轴与l2相交于点C，设l1、l2与BC围成的阴影部分面积为S，解答下列问题：
30、如图，抛物线L1：y=-x2-2x+3交x轴于A，B两点，交y轴于M点．将抛物线L1向右平移2个单位后得到抛物线L2，L2交x轴于C，D两点．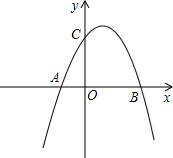
如图，抛物线L1：y=-x2-4x+5交x轴于A、B，交y轴于C，顶点为D．
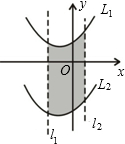如图将抛物线L1：y=x2+2x+3向下平移10个单位得L2，而l1、l2的表达式分别是l1：x=-2，l2：
如图，抛物线l1：y1=a（x+1）2+2与l2：y2=-（x-2）2-1交于点B（1，-2），且分别与y轴交于点D、E．过点B作x轴的平行线，交抛物线于点A、C，则以下结论：