Question

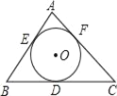
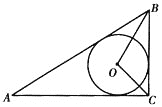
【题目】已知：如图，⊙O内切于△ABC，∠BOC=105°，∠ACB=90°，AB=20cm．求BC、AC的长．

Answer 1

【答案】BC、AC的长分别是10cm、cm.

【解析】

先根据 O内切于△ABC，得出∠ABO=∠CBO，∠BCO=∠ACO，再根据∠ACB=90°，得出∠BCO=45°，再根据三角形内角和定理得出∠OBC的度数，从而求出∠ABC和∠A的度数，即可求出BC的长，再根据勾股定理即可求出AC．

解：∵圆O内切于△ABC，

∴∠ABO=∠CBO，∠BCO=∠ACO，

∵∠ACB=90°，

∴∠BCO=×90°=45°，

∵∠BOC=105°，

∴∠CBO=180°45°105°=30°，

∴∠ABC=2∠CBO=60°，

∴∠A=30°，

∴BC=AB=×20=10cm，

∴AC=

∴BC、AC的长分别是10cm、cm.