题目内容
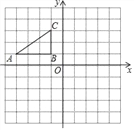
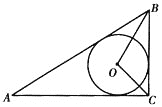
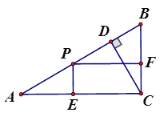
【题目】如图,在△ABC中,∠C=90°,CD⊥AB,垂足为D,AC=20,BC=15.动点P从A开始,以每秒2个单位长的速度沿AB方向向终点B运动,过点P分别作AC、BC边的垂线,垂足为E、F.
(1)求AB与CD的长;
(2)当矩形PECF的面积最大时,求点P运动的时间t;
(3)以点C为圆心,r为半径画圆,若圆C与斜边AB有且只有一个公共点时,求r的取值范围.
【答案】(1)25,12;(2)6.25;(3)r=12,15<r≤20.
【解析】
试题(1)在Rt△ABC中,先利用勾股定理求出AB的长,然后由面积关系求出CD的长;
(2)由相似关系可以求出PE、CE与t的关系,矩形PECF的面积最大,求点P运动的时间t;
(3)当圆与AB相切时,r=12,当圆与AB相交且只有一个交点时,15<r≤20.
试题解析:(1)在Rt△ABC中,AC=20,BC=15
∴![]()
又![]()
∴![]()
(2)∵△APE∽△ABC,
∴![]()
∴![]() ,即
,即![]() ,
,
同理可求:![]()
设矩形PECF的面积为S,S="1.2t(20-1.6t)" ,当t=6.25时,S有最大值.
(3)当圆与AB相切时,r=12,当圆与AB相交且只有一个交点时,15<r≤20.
考点: 1.勾股定理;2.二次函数;3.直线与圆的位置关系.

练习册系列答案
相关题目