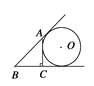Question

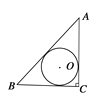
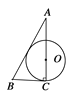
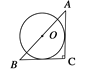
【题目】如图，PA、PB、CD分别切⊙O于A、B、E，CD交PA、PB于C、D两点，若∠P=40°，则∠PAE+∠PBE的度数为（　　）

A. 50° B. 62° C. 66° D. 70°

Answer 1

【答案】D

【解析】

由PA、PB、CD分别切⊙O于A、B、E，CD交PA、PB于C、D两点，根据切线长定理即可得：CE=CA，DE=DB，然后由等边对等角与三角形外角的性质，可求得∠PAE= ∠PCD，∠PBE= ∠PDC，继而求得∠PAE+∠PBE的度数．

∵PA、PB、CD分别切⊙O于A. B.E，CD交PA、PB于C.D两点，

∴CE=CA，DE=DB，

∴∠CAE=∠CEA，∠DEB=∠DBE，

∴∠PCD=∠CAE+∠CEA=2∠CAE，∠PDC=∠DEB+∠DBE=2∠DBE，

∴∠CAE=∠PCD，∠DBE=∠PDC，

即∠PAE=∠PCD，∠PBE=∠PDC，

∵∠P=40，

∴∠PAE+∠PBE=∠PCD+∠PDC=(∠PCD+∠PDC)=(180∠P)=70.

故答案选：D.