题目内容
 已知:直线y=-2x-2与x轴交于点A,与y轴交于点C,抛物线经过点A、C、E,且点E(6,7)
已知:直线y=-2x-2与x轴交于点A,与y轴交于点C,抛物线经过点A、C、E,且点E(6,7)(1)求抛物线的解析式.
(2)在直线AE的下方的抛物线取一点M使得构成的△AME的面积最大,请求出M点的坐标及△AME的最大面积.
(3)若抛物线与x轴另一交点为B点,点P在x轴上,点D(1,-3),以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
分析:(1)先根据直线y=-2x-2与x轴交于点A,与y轴交于点C,求出A,C两点的坐标,再用待定系数法即可求出抛物线的解析式;
(2)在抛物线上取一点M,作MN∥y轴交AE于点N,过点E作EH⊥x轴于点H,则S△AME=
•MN•AH,而AH=7,故当MN取最大值时,△AME的面积最大.设点M的横坐标为a,则纵坐标为
a2-
a-2,先用待定系数法求出AE的解析式,得到N的坐标为(a,a+1),再用含a的代数式表示MN,然后根据二次函数的增减性求出MN的最大值;
(3)过点E作EF⊥x轴于点F,过点D作DM⊥x轴于点M.先证明△EAF与△BDM都是等腰直角三角形,得到∠EAB=∠MBD.当以点P、B、D为顶点的三角形与△AEB相似时,①过点D作∠DP1B=∠AEB交x轴于点P1,得到△ABE∽BDP1;②过点D作∠DP2B=∠ABE交x轴于点P2,得到△ABE∽△BP2D,根据相似三角形对应边成比例即可.
(2)在抛物线上取一点M,作MN∥y轴交AE于点N,过点E作EH⊥x轴于点H,则S△AME=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(3)过点E作EF⊥x轴于点F,过点D作DM⊥x轴于点M.先证明△EAF与△BDM都是等腰直角三角形,得到∠EAB=∠MBD.当以点P、B、D为顶点的三角形与△AEB相似时,①过点D作∠DP1B=∠AEB交x轴于点P1,得到△ABE∽BDP1;②过点D作∠DP2B=∠ABE交x轴于点P2,得到△ABE∽△BP2D,根据相似三角形对应边成比例即可.
解答: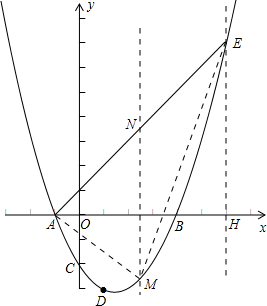 解:(1)∵直线y=-2x-2与x轴交于点A,与y轴交于点C,
解:(1)∵直线y=-2x-2与x轴交于点A,与y轴交于点C,
∴A(-1,0),C(0,-2).
设过点A、C、E三点的抛物线的解析式为y=ax2+bx+c,
则
,
解得
,
∴y=
x2-
x-2;
(2)在抛物线上取一点M,作MN∥y轴交AE于点N,过点E作EH⊥x轴于点H,则
S△AME=S△AMN+S△MNE=
MN•AH.
设点M的横坐标为a,则纵坐标为
a2-
a-2.
∵MN∥y轴,∴点N的横坐标为a.
设直线AE的解析式y=kx+b,把A(-1,0)、E(6,7)代入,
得
,解得
,
∴y=x+1.
∵N在直线AE上,∴N(a,a+1).
∴MN=a+1-(
a2-
a-2)=a+1-
a2+
a+2=-
a2+
a+3,
∴当a=
=
时,MN有最大值,此时MN=
=
,
∴S△AME=
MN•AH=
×
×7=
,M(
,-
);
(3)过点E作EF⊥x轴于点F,过点D作DM⊥x轴于点M.
∵A(-1,0),B(4,0),E(6,7),
∴AO=1,BO=4,FO=6,FE=7,AB=5,
∴AF=FE=7,∠EAB=45°,AE=
=7
.
∵D(1,-3 ),
∴DM=3,OM=1,MB=3,
∴DM=MB=3,
∴∠MBD=45°,
∴∠EAB=∠MBD,BD=
=3
.
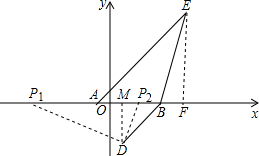 过点D作∠DP1B=∠AEB交x轴于点P1,则△ABE∽BDP1,
过点D作∠DP1B=∠AEB交x轴于点P1,则△ABE∽BDP1,
∴AE:P1B=AB:BD,即7
:P1B=5:3
,
∴P1B=
,P1O=P1B-OB=
-4=
,
∴P1(-
,0);
过点D作∠DP2B=∠ABE交x轴于点P2,则△ABE∽△BP2D,
∴DB:AE=P2B:AB,即3
:7
=P2B:5,
∴P2B=
,P2O=OB-P2B=4-
=
,
∴P2(
,0).
 解:(1)∵直线y=-2x-2与x轴交于点A,与y轴交于点C,
解:(1)∵直线y=-2x-2与x轴交于点A,与y轴交于点C,∴A(-1,0),C(0,-2).
设过点A、C、E三点的抛物线的解析式为y=ax2+bx+c,
则
|
解得
|
∴y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)在抛物线上取一点M,作MN∥y轴交AE于点N,过点E作EH⊥x轴于点H,则
S△AME=S△AMN+S△MNE=
| 1 |
| 2 |
设点M的横坐标为a,则纵坐标为
| 1 |
| 2 |
| 3 |
| 2 |
∵MN∥y轴,∴点N的横坐标为a.
设直线AE的解析式y=kx+b,把A(-1,0)、E(6,7)代入,
得
|
|
∴y=x+1.
∵N在直线AE上,∴N(a,a+1).
∴MN=a+1-(
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴当a=
-
| ||
2×(-
|
| 5 |
| 2 |
4×(-
| ||||
4×(-
|
| 49 |
| 8 |
∴S△AME=
| 1 |
| 2 |
| 1 |
| 2 |
| 49 |
| 8 |
| 343 |
| 16 |
| 5 |
| 2 |
| 21 |
| 8 |
(3)过点E作EF⊥x轴于点F,过点D作DM⊥x轴于点M.
∵A(-1,0),B(4,0),E(6,7),
∴AO=1,BO=4,FO=6,FE=7,AB=5,
∴AF=FE=7,∠EAB=45°,AE=
| AF2+EF2 |
| 2 |
∵D(1,-3 ),
∴DM=3,OM=1,MB=3,
∴DM=MB=3,
∴∠MBD=45°,
∴∠EAB=∠MBD,BD=
| MB2+MD2 |
| 2 |
 过点D作∠DP1B=∠AEB交x轴于点P1,则△ABE∽BDP1,
过点D作∠DP1B=∠AEB交x轴于点P1,则△ABE∽BDP1,∴AE:P1B=AB:BD,即7
| 2 |
| 2 |
∴P1B=
| 42 |
| 5 |
| 42 |
| 5 |
| 22 |
| 5 |
∴P1(-
| 22 |
| 5 |
过点D作∠DP2B=∠ABE交x轴于点P2,则△ABE∽△BP2D,
∴DB:AE=P2B:AB,即3
| 2 |
| 2 |
∴P2B=
| 15 |
| 7 |
| 15 |
| 7 |
| 13 |
| 7 |
∴P2(
| 13 |
| 7 |
点评:本题着重考查了待定系数法求二次函数解析式、二次函数的最值、相似三角形的判定和性质,三角形的面积等知识点,综合性较强,考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
 已知:直线y=-2x+4交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线y=ax2+bx+c(a≠0)经过点A、B、C.
已知:直线y=-2x+4交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线y=ax2+bx+c(a≠0)经过点A、B、C.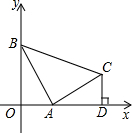 已知:直线y=-2x+2分别与x轴、y轴相交于点A、B,以线段AB为直角边在第一象限内作等腰直角△ABC,∠BAC=90°,过C作CD⊥x轴于D.求:
已知:直线y=-2x+2分别与x轴、y轴相交于点A、B,以线段AB为直角边在第一象限内作等腰直角△ABC,∠BAC=90°,过C作CD⊥x轴于D.求: 已知,直线y=2x+3与直线y=-2x-1.
已知,直线y=2x+3与直线y=-2x-1.