题目内容
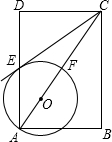
 如图,在矩形ABCD中,对角线AC,BD相交于点G,E为AD的中点.连接BE交AC于点F,连接FD.若∠BFA=90°,则下列四对三角形:(1)△BEA与△ACD;(2)△FED与△DEB;(3)△CFD与△ABG;(4)△ADF与△CFB,其中相似的有
如图,在矩形ABCD中,对角线AC,BD相交于点G,E为AD的中点.连接BE交AC于点F,连接FD.若∠BFA=90°,则下列四对三角形:(1)△BEA与△ACD;(2)△FED与△DEB;(3)△CFD与△ABG;(4)△ADF与△CFB,其中相似的有
- A.(1)(4)
- B.(1)(2)
- C.(2)(3)(4)
- D.(1)(2)(3)
D
分析:根据题意,分别寻找各对三角形相似的条件,运用判定方法判断.∠EFC=∠ADC=90°
∴∠DCA+∠FED=180°
∵∠FED+∠AEB=180°
∴∠AEB=∠DCA,∠CDA=∠DAB=90°
∵∠DAC=∠ABE∴△BEA∽△ACD.
再利用相似三角形相似的判定证明△FED与△DEB,△CFD与△ABG相似,而(4)不成立.
解答:(1)∵矩形ABCD,∴∠EAB=∠CDA=90°,
∴∠BAF+∠CAD=90°,
又∠BFA=90°,∴∠BAF+∠ABF=90°,
∴∠CAD=∠ABF,
∴△BEA与△ACD相似;故此选项正确;
(2)△FED与△DEB相似.理由:DE2=AE2=EF•EB,∠DEF=∠BED;故此选项正确;
(3)△CFD与△ABG相似.理由:∠CDF=90°-∠EDF,∠AGB=90°-∠EBG,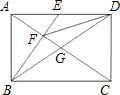
由(2)的结论得:∠EDF=∠EBD,故∠CDF=∠AGB;∵AB∥CD,∴∠DCF=∠BAG;故此选项正确;
(4)△ADF与△CFB不具备相似条件.
故选D.
点评:本题主要考查了三角形相似的判定.
分析:根据题意,分别寻找各对三角形相似的条件,运用判定方法判断.∠EFC=∠ADC=90°
∴∠DCA+∠FED=180°
∵∠FED+∠AEB=180°
∴∠AEB=∠DCA,∠CDA=∠DAB=90°
∵∠DAC=∠ABE∴△BEA∽△ACD.
再利用相似三角形相似的判定证明△FED与△DEB,△CFD与△ABG相似,而(4)不成立.
解答:(1)∵矩形ABCD,∴∠EAB=∠CDA=90°,
∴∠BAF+∠CAD=90°,
又∠BFA=90°,∴∠BAF+∠ABF=90°,
∴∠CAD=∠ABF,
∴△BEA与△ACD相似;故此选项正确;
(2)△FED与△DEB相似.理由:DE2=AE2=EF•EB,∠DEF=∠BED;故此选项正确;
(3)△CFD与△ABG相似.理由:∠CDF=90°-∠EDF,∠AGB=90°-∠EBG,

由(2)的结论得:∠EDF=∠EBD,故∠CDF=∠AGB;∵AB∥CD,∴∠DCF=∠BAG;故此选项正确;
(4)△ADF与△CFB不具备相似条件.
故选D.
点评:本题主要考查了三角形相似的判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
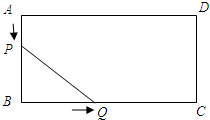 如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )
如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )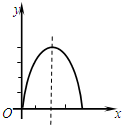
 .
.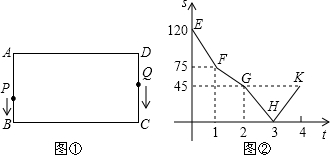 动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.
动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.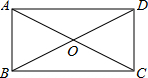 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( )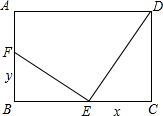 DE,EF与AB交于点F,设CE=x,BF=y.
DE,EF与AB交于点F,设CE=x,BF=y.