题目内容
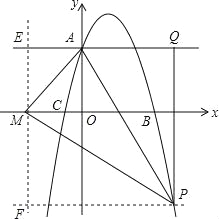
【题目】已知抛物线y=﹣x2+3x+4交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l.在位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q.连接AP.
(1)写出A,B,C三点的坐标;
(2)若点P位于抛物线的对称轴的右侧:
①如果以A,P,Q三点构成的三角形与△AOC相似,求出点P的坐标;
②若将△APQ沿AP对折,点Q的对应点为点M.是否存在点P,使得点M落在x轴上?若存在,求出点P的坐标;若不存在,请说明理由;
③设AP的中点是R,其坐标是(m,n),请直接写出m和n的关系式,并写出m的取值范围.

【答案】(1)B(4,0),C(﹣1,0)(2)①P(![]() ,
,![]() )或(7,24)②P(4,0)或(5,﹣6)③m<0,或m>
)或(7,24)②P(4,0)或(5,﹣6)③m<0,或m>![]()
【解析】
试题分析:(1)先令x=0求出y的值即可得出A点坐标,再令y=0求出x的值即可得出BC两点的坐标;
(2)①分△AQP∽△AOC与△AQP∽△COA两种情况进行讨论;
②过点M作y轴的平行线交直线AQ于点E,过点P作PF⊥直线ME于点F,设Q(x,4),则P(x,﹣x2+3x+4),PQ=x2﹣3x=PM,再由△AEM∽△MFP求出PF的表达式,在Rt△AOM中根据勾股定理求出x的值,进而可得出P点坐标
③根据在位于直线l下方的抛物线上任取一点P,则有a<0或a>3,由点P在抛物线上即可建立m与n的关系.
试题解析:(1)∵令x=0,则y=4,
∴A(0,4);
∵令y=0,则﹣x2+3x+4=0,解得x1=4,x2=﹣1,
∴B(4,0),C(﹣1,0);
(2)①∵以A,P,Q三点构成的三角形与△AOC相似,
∴△AQP∽△AOC与△AQP∽△COA,
∴![]() 或
或![]() ,
,
即![]() 或
或![]() ,
,
解得x=![]() 或x=7,均在对称轴的右侧,
或x=7,均在对称轴的右侧,
∴P(![]() ,
,![]() )或(7,24);
)或(7,24);
②如图所示,过点M作y轴的平行线交直线AQ于点E,过点P作PF⊥直线ME于点F,
设Q(x,4),则P(x,﹣x2+3x+4),PQ=x2﹣3x=PM,
∵∠EAM+∠EMA=90°,∠EMA+∠FMP=90°,
∴∠FMP=∠EAM.
∵∠MFP=∠AEM=90°,
∴△AEM∽△MFP,
∴![]() .
.
∵MP=x2﹣3x,
∴![]() ,
,
∴PF=4x﹣12,
∴OM=(4x﹣12)﹣x=3x﹣12,
在Rt△AOM中,
∵OM2+OA2=AM2,即(3x﹣12)2+42=x2,解得x1=4,x2=5均在抛物线对称轴的右侧,
∴P(4,0)或(5,﹣6).
③∵抛物线y=﹣x2+3x+4和A(0,4),
∴抛物线和直线l的交点坐标为A(0,4),(3,4),
设P(a,﹣a2+3a+4);(a<0或a>3)
∵AP的中点是R,A(0,4),
∴![]() =m,
=m,![]() =n,
=n,
∴n=﹣2m2+3m+4,
∵a<0或a>3,
∴2m<0,或2m>3,
∴m<0,或m>![]() .
.

 阅读快车系列答案
阅读快车系列答案