题目内容
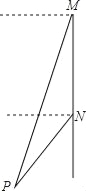
【题目】如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )
A.22.48
B.41.68
C.43.16
D.55.63
【答案】B
【解析】
试题分析:过点P作PA⊥MN于点A,则若该船继续向南航行至离灯塔距离最近的位置为PA的长度,利用锐角三角函数关系进行求解即可,如图,过点P作PA⊥MN于点A,MN=30×2=60(海里),
∵∠MNC=90°,∠CPN=46°,∴∠MNP=∠MNC+∠CPN=136°,∵∠BMP=68°,
∴∠PMN=90°﹣∠BMP=22°,∴∠MPN=180°﹣∠PMN﹣∠PNM=22°, ∴∠PMN=∠MPN,
∴MN=PN=60(海里), ∵∠CNP=46°,∴∠PNA=44°,
∴PA=PN·sin∠PNA=60×0.6947≈41.68(海里)


练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目