Question

【题目】在平面直角坐标系中，A（﹣4，0），点C是y轴正半轴上的一点，且∠ACB＝90°，AC＝BC

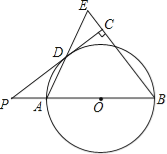
（1）如图①，若点B在第四象限，C（0，2），求点B的坐标；

（2）如图②，若点B在第二象限，以OC为直角边在第一象限作等腰Rt△COF，连接BF，交y轴于点M，求CM的长．

Answer 1

【答案】(1) B点坐标（2，﹣2）；(2)2

【解析】

（1）作BD⊥CO，根据同角的余角相等可得∠BCD＝∠CAO，然后证明ACO≌△CBD，根据全等三角形对应边相等的性质即可解题；

（2）作BG⊥y轴，根据同角的余角相等可得∠CAO＝∠BCG，然后证明△CAO≌△BCG，可得CG＝AO＝4，BG＝OC，进而得到CF＝BG，然后再证明△BGM≌△FCM，根据全等三角形的性质定理即可得到结论．

（1）作BD⊥CO，

∵∠ACB＝90°，

∴∠BCD+∠ACO＝90°，∠ACO+∠CAO＝90°，

∴∠BCD＝∠CAO，

在△ACO和△CBD中，，

∴△ACO≌△CBD（AAS），

∴CD＝AO＝4，BD＝CO＝2，

∴OD＝2，

∴B点坐标为（2，﹣2）；

（3）作BG⊥y轴，

∵∠CAO+∠OCA＝90°，∠OCA+∠BCG＝90°，

∴∠CAO＝∠BCG，

在△CAO和△BCG中，，

∴△CAO≌△BCG（AAS），

∴CG＝AO＝4，BG＝OC，

∵OC＝CF，

∴CF＝BG，

在△BGM和△FCM中，，

∴△BGM≌△FCM（AAS），

∴MC＝MG，

∴MC＝CG＝2．