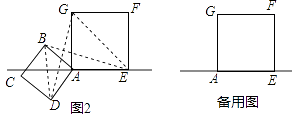Question

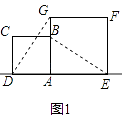
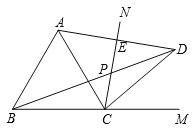
【题目】如图，CN是等边△ABC的外角∠ACM内部的一条射线，点A关于CN的对称点为D，连接AD，BD，CD，其中AD，BD分别交射线CN于点E，P．

（1）求证：CD=CB；

（2）若∠ACN= a，求∠BDC的大小（用含a的式子表示）；

（3）请判断线段PB，PC与PE三者之间的数量关系，并证明你的结论.

Answer 1

【答案】（1）见解析；（2）∠BDC=60°－a;（3）PB=PC+2PE，理由见解析

【解析】

(1)根据条件得到CN是AD的垂直平分线，证明△ABC为等边三角形即可解答.

(2)求出△ABC是等边三角形，转换角度即可解答.

(3) 在PB上截取PF使PF=PC，连接CF,利用三角形全等解答.

（1）证明：∵点A与点D关于CN对称，

∴CN是AD的垂直平分线，

∴CA=CD，

∵△ABC为等边三角形，

∴CB=CA，

∴CD=CB

（2）解：由（1）可知：CA=CD，CN⊥AD，

∴∠ACD=2∠ACN=2α．

∵△ABC是等边三角形，

∴∠ACB=60°，

∴∠BCD=∠ACB+∠ACD=60°+2 ．

∵CB=CD，

∴∠BDC=∠DBC= （180°-∠BCD）=60°-α．

（3）解：证明：结论：PB=PC+2PE在PB上截取PF使PF=PC，连接CF．

∵CA=CD，∠ACD=2 ，

∴∠CDA=∠CAD=90°-α，

∵∠BDC=60°-α，

∴∠PDE=∠CDA-∠BDC=30°，

∴在Rt△DPE中，PD=2PE．

∵∠CPF=∠DPE=90°-∠PDE=60°，

∴△CPF是等边三角形，

∴∠CPF=∠CFP=60°，

∴∠BFC=∠DPC=120°，

在△BFC和△DPC中，

∵ ，

∴△BFC≌△DPC．

∴BF=PD=2PE．

∴PB= PF+BF=PC+2PE