题目内容
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为 ![]() 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.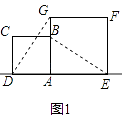
(1)图1中,小明发现DG=BE,请你帮他说明理由.
(2)小明将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,请你直接写出此时BE的长.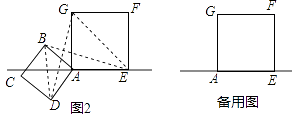
【答案】
(1)解:如图1, 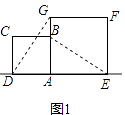 ∵四边形ABCD与四边形AEFG都是正方形,
∵四边形ABCD与四边形AEFG都是正方形,
∴AD=AB,AG=AE,∠DAG=∠BAE=90°.
在△DAG与△BAE中,
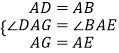 ,
,
∴△DAG≌△BAE,
∴DG=BE;
(2)解:将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,分两种情况:
①如果C在EA的延长线上时,
如备用图1, 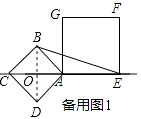
连结BD交AC于O,
∵正方形ABCD边长为 ![]() ,
,
∴BD=AC= ![]() AB=2,AC⊥BD,
AB=2,AC⊥BD,
∴OB=OA= ![]() BD=1.
BD=1.
∵正方形AEFG边长为2,
∴OE=OA+AE=1+2=3.
在Rt△BOE中,∵∠BOE=90°,
∴BE= ![]() =
= ![]() =
= ![]() ;
;
②如果C在AE上时,
如备用图2, 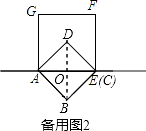
连结BD交AC于O,
∵正方形ABCD边长为 ![]() ,
,
∴BC=AC= ![]() AB=2,
AB=2,
∵正方形AEFG边长为2,
∴AE=2,
∴C与E重合,
∴BE=BC= ![]() .
.
故所求BE的长为 ![]() 或
或 ![]() .
.
【解析】(1)由正方形的性质可判定△DAG≌△BAE,得出DG=BE;(2)C恰好落在直线l上分两类:C在EA的延长线上;C在AE上时;可由勾股定理和正方形的性质求出.
【考点精析】本题主要考查了图形的旋转的相关知识点,需要掌握每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素才能正确解答此题.