题目内容
【题目】问题探究
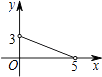
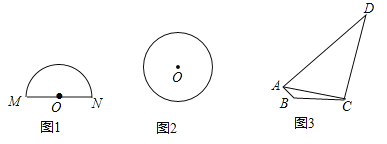
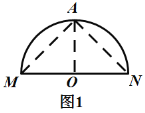
(1)如图1,请在半径为![]() 的半圆
的半圆![]() 内(含弧和直径
内(含弧和直径![]() )画出面积最大的三角形,并求出这个三角形的面积;
)画出面积最大的三角形,并求出这个三角形的面积;
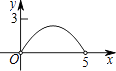
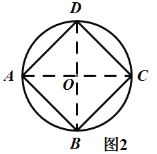
(2)如图2,请在半径为![]() 的
的![]() 内(含弧)画出面积最大的矩形
内(含弧)画出面积最大的矩形![]() ,并求出这个矩形的面积;
,并求出这个矩形的面积;
问题解决
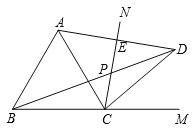
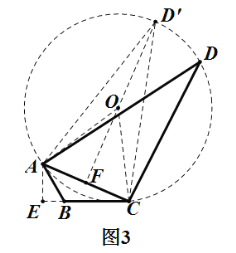
(3)如图3,![]() 是一块草坪,其中
是一块草坪,其中![]() ,
,![]() ,
,![]() ,某开发商现准备再征一块地,把
,某开发商现准备再征一块地,把![]() 扩充为四边形
扩充为四边形![]() ,使
,使![]() ,是否存在面积最大的四边形
,是否存在面积最大的四边形![]() ?若存在,求出四边形
?若存在,求出四边形![]() 的最大面积;若不存在,请说明理由.(结果保留根号)
的最大面积;若不存在,请说明理由.(结果保留根号)
【答案】(1)图形见解析;![]() ;(2)图形见解析;
;(2)图形见解析;![]() 矩形
矩形![]() ;(3)存在,最大面积为
;(3)存在,最大面积为![]() .
.
【解析】
(1)过圆心O作直径的垂线得到最大的![]() ,求面积即可;
,求面积即可;
(2)作两条互相垂直的直径,作对角线,连成的四边形即为最大的矩形,求其面积即可;
(3)如图3,过A作AE⊥BC,交CB的延长线于E,分别求出EC、AE、AC的长,求![]() 的面积,在
的面积,在![]() 中,AC是定值,∠D=30°是定值,画
中,AC是定值,∠D=30°是定值,画![]() 的外接圆O,由图3可知:当D点与AC的距离最大时,
的外接圆O,由图3可知:当D点与AC的距离最大时,![]() 的面积最大,设AC的中垂线交⊙O于
的面积最大,设AC的中垂线交⊙O于![]() ,交AC于F,则
,交AC于F,则![]() 即为D点与AC的最大距离,求出
即为D点与AC的最大距离,求出![]() ,代入面积公式求面积即可.
,代入面积公式求面积即可.
解:(1)如图1,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() 即为所求.
即为所求.
![]()
(2)如图2,过点![]() 作
作![]() 的任一直径
的任一直径![]() ,再过点
,再过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,则矩形
,则矩形![]() 即为所求.
即为所求.
![]() 矩形
矩形![]() ;
;
(3)存在面积最大的四边形![]() ,理由如下:
,理由如下:
如图3,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() .
.
![]() ,
,
![]() .
.
在![]() 中,
中,![]() 是定值,
是定值,![]() 是定值,
是定值,
如图3,![]() 、
、![]() 、
、![]() 三点在同一
三点在同一![]() 上(作
上(作![]() 、
、![]() 的中垂线,交点即为圆心
的中垂线,交点即为圆心![]() ),
),
![]() 的长度一定,
的长度一定,
![]() 当
当![]() 点与
点与![]() 的距离最大时,
的距离最大时,![]() 的面积最大.
的面积最大.
设![]() 的中垂线交
的中垂线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,
则![]() 即为
即为![]() 点与
点与![]() 的最大距离.
的最大距离.
![]() ,
,
连接![]() 、
、![]() ,则
,则![]() 。
。
![]() 是等边三角形.
是等边三角形.
![]() ,
,![]() .
.
∴![]() .
.
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]()
即四边形![]() 的最大面积为
的最大面积为![]() .
.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目