题目内容
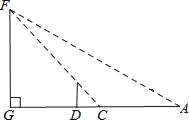
【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆GF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.
(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上, ![]() ,
, ![]() ,结果精确到0.1)
,结果精确到0.1)
【答案】(1)![]() a-2;(2)旗杆GF的高度约12.5米.
a-2;(2)旗杆GF的高度约12.5米.
【解析】试题分析:
(1)根据△CDE∽△CGF先求得CG的长,再求DG;
(2)先用FG表示出AG的长,再在Rt△AFG中用∠A=30°,借助三角形函数列方程求解.
试题解析:
解:(1)∵由题意知,FG∥DE,
∴△CDE∽△CGF,
∴![]() ,即
,即![]() ,
,
∴GD=![]() a-2;
a-2;
(2)如图所示:
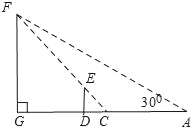
在直角△AFG中,∠A=30°,AG=![]() FG+6,
FG+6,
∵tanA=![]() ,tan30°=
,tan30°=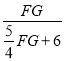 ,
,
即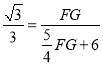 ,
,
解得fG≈12.5.
答:电线杆FG的高度约12.5米.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目