Question

已知如图：矩形ABCD的边BC在x轴上，E为对角线BD的中点，点B、D的坐标分别为B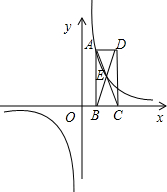（1，0），D（3，3），反比例函数y=

k

x

的图象经过A点，
（1）写出点A和点E的坐标；
（2）求反比例函数的解析式；
（3）判断点E是否在这个函数的图象上．

Answer 1

分析：（1）因为四边形ABCD是矩形，所以点A横坐标与点B相同，纵坐标与点D相同；因为E为对角线BD的中点，所以点E纵坐标为点A纵坐标一半，横坐标为

1

2

BC与点B横坐标之和；
（2）设y=

k

x

，由反比例函数y=

k

x

的图象经过A点，所以k=1×3=3，即解；
（3）欲判断点E是否在这个函数的图象上，就看其坐标是不是方程y=

3

x

的解．

解答：（1）解：∵B（1，0），D（3，3），E为对角线BD的中点
∴点E坐标为（2，

3

2

），
又∵四边形ABCD是矩形
∴点A的横坐标等于点B的横坐标，点A的纵坐标等于点D的纵坐标，
故点A坐标为：（1，3）．
（2）解：设所求的函数关系式为y=

k

x

，
把x=1，y=3代入，得：k=3×1=3，
∴y=

3

x

为所求的解析式．
（3）解：当x=2时，y=

3

2

∴点E（2，

3

2

）在这个函数的图象上．

点评：此题难度中等，考查反比例函数的图象和性质及矩形性质．同学们要熟练掌握此类题型．