题目内容
 (2013•阜宁县一模)已知抛物线的顶点(-1,-4)且过点(0,-3),直线l是它的对称轴.
(2013•阜宁县一模)已知抛物线的顶点(-1,-4)且过点(0,-3),直线l是它的对称轴.(1)求此抛物线的解析式;
(2)设抛物线交x轴于点A、B(A在B的左边),交y轴于点C,P为l上的一动点,当△PBC的周长最小时,求P点的坐标;
(3)在直线l上是否存在点M,使△MBC是等腰三角形?若存在,直接写出符合条件的点M的坐标;若不存在请说明理由.
分析:(1)设抛物线顶点式解析式y=a(x+1)2-4,然后把点(0,-3)代入求出a的值,即可得解;
(2)先求出点B、C的坐标,再根据轴对称确定最短路线问题求出点C关于直线l的对称点C′,然后利用待定系数法求一次函数解析式求出直线BC′的解析式,然后令x=-1求解即可;
(3)先根据勾股定理求出BC2,设点M的坐标为(-1,y),然后分MC=BC,MB=BC,MB=MC三种情况,利用勾股定理列式计算即可得解.
(2)先求出点B、C的坐标,再根据轴对称确定最短路线问题求出点C关于直线l的对称点C′,然后利用待定系数法求一次函数解析式求出直线BC′的解析式,然后令x=-1求解即可;
(3)先根据勾股定理求出BC2,设点M的坐标为(-1,y),然后分MC=BC,MB=BC,MB=MC三种情况,利用勾股定理列式计算即可得解.
解答:解:(1)设抛物线顶点式解析式y=a(x+1)2-4,
∵抛物线经过点(0,-3),
∴a(0+1)2-4=-3,
解得a=1,
∴抛物线的解析式为y=(x+1)2-4;
(2)令y=0,则(x+1)2-4=0,
解得x1=-3,x2=1,
∴B(1,0),
令x=0,则(0+1)2-4=-3,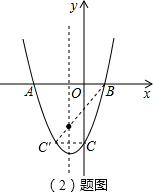
∴C(0,-3),
如图所示,直线l的对称轴为x=-1,
点C关于直线l的对称点C′(-2,-3),
设直线BC′的解析式为y=kx+b,
则
,
解得
,
∴y=x-1,
令x=-1,则y=-1-1=-2,
点P(-1,-2);
(3)∵B(1,0),C(0,-3),
∴BC2=12+32=10,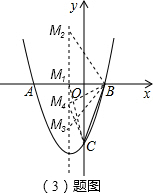
设点M(-1,y),
①MC=BC时,MC2=12+(y+3)2=10,
解得y=0或y=-6(M、B、C三点共线,舍去),
此时,点M1(-1,0),
②MB=BC时,MB2=[1-(-1)]2+y2=10,
解得y=±
,
此时点M2(-1,
),M3(-1,-
),
③MB=MC时,[1-(-1)]2+y2=12+(y+3)2,
解得y=-1,
此时点M4(-1,-1),
综上所述,点M的坐标为M1(-1,0),M2(-1,
),M3(-1,-
),M4(-1,-1).
∵抛物线经过点(0,-3),
∴a(0+1)2-4=-3,
解得a=1,
∴抛物线的解析式为y=(x+1)2-4;
(2)令y=0,则(x+1)2-4=0,
解得x1=-3,x2=1,
∴B(1,0),
令x=0,则(0+1)2-4=-3,

∴C(0,-3),
如图所示,直线l的对称轴为x=-1,
点C关于直线l的对称点C′(-2,-3),
设直线BC′的解析式为y=kx+b,
则
|
解得
|
∴y=x-1,
令x=-1,则y=-1-1=-2,
点P(-1,-2);
(3)∵B(1,0),C(0,-3),
∴BC2=12+32=10,

设点M(-1,y),
①MC=BC时,MC2=12+(y+3)2=10,
解得y=0或y=-6(M、B、C三点共线,舍去),
此时,点M1(-1,0),
②MB=BC时,MB2=[1-(-1)]2+y2=10,
解得y=±
| 6 |
此时点M2(-1,
| 6 |
| 6 |
③MB=MC时,[1-(-1)]2+y2=12+(y+3)2,
解得y=-1,
此时点M4(-1,-1),
综上所述,点M的坐标为M1(-1,0),M2(-1,
| 6 |
| 6 |
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,利用轴对称确定最短路线问题,勾股定理的应用,等腰三角形的性质,(3)难点在于要根据腰长的不同进行讨论.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 (2013•阜宁县一模)如图,在△ABC中,∠A=70°,∠C=60°,D、E分别是AB、AC上的点,且DE∥BC,则∠ADE的度数为( )
(2013•阜宁县一模)如图,在△ABC中,∠A=70°,∠C=60°,D、E分别是AB、AC上的点,且DE∥BC,则∠ADE的度数为( )