Question

【题目】写出命题“等腰三角形底边上的中点到两腰的距离相等”的逆命题，并证明该逆命题是真命题．

Answer 1

【答案】证明见解析

【解析】试题分析：

读懂“原命题”，分清“原命题的题设和结论”，交换“题设”和“结论”，并用通顺、简洁的语句写出“逆命题”；然后画出符合“逆命题”题意的图形，改写出“已知”和“求证”事项，最后完成证明.

试题解析：

逆命题：如果一个三角形一边上的中点到另两边的距离相等，那么这个三角形是等腰三角形．

已知：如图，在△ABC中，D是BC的中点，DE⊥AB于点E，DF⊥AC于点F，且DE＝DF.

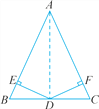
求证：△ABC为等腰三角形．

证明：连结AD.

∵ D是BC的中点，

∴S△ABD＝S△ACD.

∵DE⊥AB，DF⊥AC，

∴S△ABD＝AB·DE，S△ACD＝AC·DF.

又∵DE＝DF，

∴AB＝AC，

∴△ABC为等腰三角形．