��Ŀ����
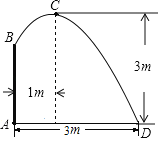
����Ŀ��ij����Ϊ������һ�����͡���ˮ�ϰѡ���������������˵��飬�������ÿ��������y��ֻ�������۵���x��Ԫ������һ�κ�����ϵ��������IJ����������������֪ÿֻ����Ϊ10Ԫ�����۵���Ϊ������ÿֻ�������۵��۩����ۣ�
���۵���x��Ԫ�� | 20 | 22 | 25 | �� |
�����۶�y��ֻ�� | 300 | 280 | 250 | �� |
��1�����y��x֮��ĺ�������ʽ
��2�������͡���ˮ�ϰѡ�ÿ�µ�������Ϊw��Ԫ������w����x�ĺ�������ʽ����ָ�����۵���Ϊ����Ԫʱ���������������Ƕ���Ԫ��
���𰸡���1��y����10x+500����2�������۵��۶�Ϊ30Ԫʱ��ÿ�¿ɻ���������4000Ԫ��
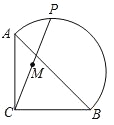
��������
��1��ֱ�����ô���ϵ������������ʽ��
��2��������=��������������������ȱ�ʾ��w���ٸ��ݶ��κ�������ֵ��������䷽���ɣ�
�⣺��1����y��kx+b��k��0����
�������⣬����㣨20��300������25��250����
�� ![]() ��
��
��ã�![]() ��
��
��y����10x+500��
��2��������ã�w����x��10������10x+500������10x2+600x��5000����10��x��30��2+4000��
��a����10��0��
�൱x��30ʱ��w�����ֵ4000��
�������۵��۶�Ϊ30Ԫʱ��ÿ�¿ɻ���������4000Ԫ��

 ��ս100��Ԫ����Ծ�ϵ�д�
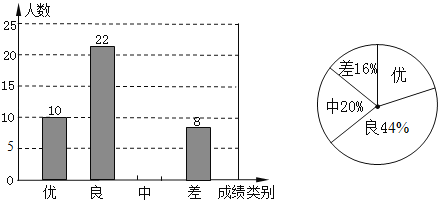
��ս100��Ԫ����Ծ�ϵ�д�����Ŀ������5�·ݣ�ʮ���о��꼶ѧ���μ����п�����ģ�⿼�ԣ�Ϊ���˽��У���꼶��1����ͬѧ���п������������ȫ��ѧ�����п������ɼ�������ͳ�ƣ����������²�������Ƶ���ֲ���������ͳ��ͼ������ͼ���е���Ϣ����������⣺
���� | �����Σ��֣��� | Ƶ�� |
A | 26��x��31 | 2 |
B | 31��x��36 | 5 |
C | 36��x��41 | 15 |
D | 41��x��46 | m |
E | 46��x��51 | 10 |
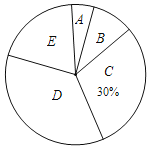
��1����ȫ��ѧ��������m��ֵ��
��2��������ͳ��ͼ�е�E��Ӧ������Բ�ĽǵĶ�����
��3���ð��п������ɼ����ֹ���3�ˣ���������2�ˣ�Ů��1�ˣ��������3�������ѡȡ2�˵����꼶���о��齻�������á��б���������״ͼ�������ǡ��ѡ��һ��һŮ�ĸ��ʣ�